题目内容
2．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$，点P（2，1）在C的渐近线上，则C的率心率为$\frac{\sqrt{5}}{2}$．分析 利用点在曲线上，推出a、b关系，求解双曲线的离心率 即可．
解答 解：双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$，点P（2，1）在C的渐近线上，
可得：$\frac{2}{a}-\frac{1}{b}=0$，可得$\frac{4}{{a}^{2}}=\frac{1}{{c}^{2}-{a}^{2}}$，
即：4c2-4a2=a2，
∴e=$\frac{\sqrt{5}}{2}$
故答案为：$\frac{\sqrt{5}}{2}$．
点评 本题考查双曲线的简单性质的应用，考查计算能力．
练习册系列答案
相关题目
7．若不等式x2-ax+a≤1有解，则a的取值范围为（ ）
| A． | a＜2 | B． | a=2 | C． | a＞2 | D． | a∈R |
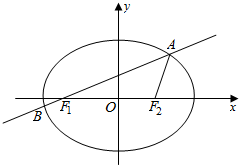如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，F1、F2为其左、右焦点，过F1的直线l交椭圆于A、B两点，△F1AF2的周长为$2（\sqrt{2}+1）$．