Question

【题目】定义在R上的奇函数y=f（x）满足f（3）=0，且当x＞0时，不等式f（x）＞﹣xf′（x）恒成立，则函数g（x）=xf（x）+lg|x+1|的零点的个数为_______.

Answer 1

【答案】3

【解析】

要求函数g（x）=xf（x）+lg|x+1|的零点的个数，可构造函数，将问题转化为函数与函数的图象的个数。根据已知条件可判断函数的单调性和奇偶性，进而画函数的图象，观察两个函数图象交点的个数即可。

令， 因为当x＞0时，不等式f（x）＞﹣xf′（x）恒成立，

所以当x＞0时，。所以函数在上为增函数。

因为y=f（x）是定义在R上的奇函数，所以。

所以函数为偶函数，且函数在上为减函数。

因为定义在R上的奇函数y=f（x）满足f（3）=0，所以。

所以。做函数与函数的图象如图所示。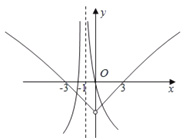

由函数的图象可知，函数与函数的图象有三个交点。

所以函数g（x）=xf（x）+lg|x+1|的零点的个数为3个。