题目内容
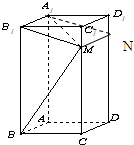
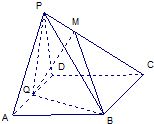
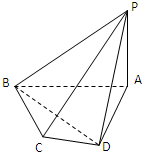
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求EF和平面ABCD所成的角α;
(Ⅲ)求异面直线EF与BD所成的角β.
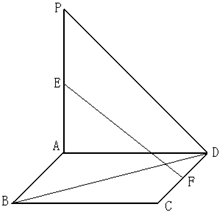
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求EF和平面ABCD所成的角α;
(Ⅲ)求异面直线EF与BD所成的角β.

解(Ⅰ)证明:由已知PA⊥AD,AB⊥AD,
所以∠PAB为平面PAD与平面ABCD所成二面角的平面角,
由已知:平面PAD⊥平面ABCD,得PA⊥AB
又AB?平面ABCD,AD?平面ABCD,且AB与AD相交
∴PA⊥平面ABCD.
(Ⅱ)连接AF,则∠AFE即为α,
在△AFE中,可求得α=arctan
(Ⅲ)取BC的中点M,连接EM、FM,则FM∥BD,
∴∠EFM(或其补角)就是异面直线EF与BD所成的角.
可求得EM=
=
,同理EF=
,又FM=
BD=
,
∴在△MFE中,cos∠EFM=
=
,
故异面直线EF与BD所成角为arccos
.
所以∠PAB为平面PAD与平面ABCD所成二面角的平面角,
由已知:平面PAD⊥平面ABCD,得PA⊥AB
又AB?平面ABCD,AD?平面ABCD,且AB与AD相交
∴PA⊥平面ABCD.
(Ⅱ)连接AF,则∠AFE即为α,
在△AFE中,可求得α=arctan
| ||
| 5 |
(Ⅲ)取BC的中点M,连接EM、FM,则FM∥BD,
∴∠EFM(或其补角)就是异面直线EF与BD所成的角.
可求得EM=
| EA2+AM2 |
| 6 |
| 6 |
| 1 |
| 2 |
| 2 |
∴在△MFE中,cos∠EFM=
| EF2+FM2-ME2 |
| 2EF•FM |
| ||
| 6 |
故异面直线EF与BD所成角为arccos
| ||
| 6 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目