题目内容
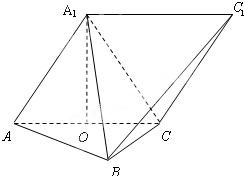
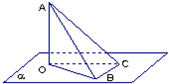
如图，AO⊥平面α，点O为垂足，BC?平面α，BC⊥OB，若∠ABO=
，∠COB=
，则cos∠BAC=______．
| π |
| 4 |
| π |
| 6 |
因为AO⊥平面α，BC?平面α，BC⊥OB，
所以根据三垂线定理可得：BC⊥AB．
设OB=2，
因为∠ABO=
，∠COB=
，
所以OA=2，AB=2
，BC=
，
所以在△ABC中有BC⊥AB，并且AB=2
，BC=
，
所以tan∠BAC=
=
，
所以cos∠BAC=
．
故答案为：
．
所以根据三垂线定理可得：BC⊥AB．
设OB=2，
因为∠ABO=
| π |
| 4 |
| π |
| 6 |
所以OA=2，AB=2
| 2 |
2
| ||
| 3 |
所以在△ABC中有BC⊥AB，并且AB=2
| 2 |
2
| ||
| 3 |
所以tan∠BAC=
| BC |
| AB |
| ||
| 6 |
所以cos∠BAC=
| ||
| 7 |
故答案为：
| ||
| 7 |
练习册系列答案
阅读快车系列答案
相关题目
