题目内容
【题目】椭圆![]() =1(a>b>0)的左右焦点分别为F1(-c,0)、F2(c,0),过椭圆中心的弦PQ满足丨PQ丨=2,∠PF2Q=90°,且△PF2Q的面积为1.
=1(a>b>0)的左右焦点分别为F1(-c,0)、F2(c,0),过椭圆中心的弦PQ满足丨PQ丨=2,∠PF2Q=90°,且△PF2Q的面积为1.
(1)求椭圆的方程;
(2)直线l不经过点A(0,1),且与椭圆交于M,N两点,若以MN为直径的圆经过点A,求证:直线l过定点,并求出该定点的坐标。
【答案】(1)![]() (2)m=-
(2)m=-![]() ,定点(0,-
,定点(0,-![]() )
)
【解析】试题分析:
(1)由题意结合几何关系可求得a2=2,b2=1,则椭圆方程是 ![]() .
.
(2)联立直线与椭圆的方程,结合韦达定理可得直线l过定点![]() .
.
试题解析:
(1)∠PF2E=90°![]() 口PF1QF2为矩形
口PF1QF2为矩形![]() 丨F1F2丨=丨PQ丨=2
丨F1F2丨=丨PQ丨=2![]() c=1
c=1
![]() =
=![]() =1
=1![]() PF1·PF2=2
PF1·PF2=2
又PF1+PF2=2a,则a2=2,b2=1
椭圆方程: ![]()
(2) 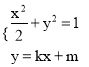
![]() (2k2+1)x2+4kmx+2(m2-1)=0
(2k2+1)x2+4kmx+2(m2-1)=0
![]()
![]() =8(2k2+1-m2),x1+x2=
=8(2k2+1-m2),x1+x2=![]() ,x1x2=
,x1x2=![]()
![]()
![]()
![]()
![]() =(x1,y1-1)
=(x1,y1-1)![]() (x2,y2-1)=0
(x2,y2-1)=0
![]() 3m2-2m-1=0
3m2-2m-1=0
又直线不经过A(0,1),所以m≠1,m=-![]() ,定点(0,-
,定点(0,-![]() )
)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目