[题目]已知函数f(x)=cos2 + sinωx﹣ 在区间内没有零点.则ω的取值范围是( )A.(0. ]B.(0. ]∪[ . )C.(0. ]D.(0. ]∪[ . ] 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知函数f（x）=cos2 + sinωx﹣ （ω＞0），x∈R，若f（x）在区间（π，2π）内没有零点，则ω的取值范围是（）
A.（0， ]
B.（0， ]∪[ ，）
C.（0， ]
D.（0， ]∪[ ， ]

【答案】B
【解析】解：函数f（x）=cos2 + sinωx﹣ = cosωx+ sinωx=sin（ωx+ ），可得T= ≥π，0＜ω≤2，f（x）在区间（π，2π）内没有零点，函数的图象如图两种类型，结合三角函数可得：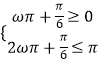
或，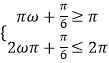

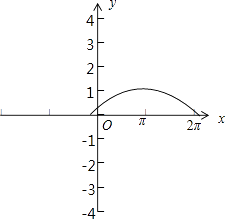
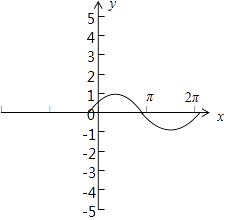
解得ω∈（0， ]∪[ ，）．
故选：B．
利用两角和与差的三角函数化简函数的解析式，利用函数的零点以及函数的周期，列出不等式求解即可．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

【题目】若y=（m﹣1）x2+2mx+3是偶函数，则f（﹣1），f（﹣ ），f（）的大小关系为（）
A.f（）＞f（）＞f（﹣1）
B.f（）＜f（﹣ ）＜f（﹣1）??
C.f（﹣ ）＜f（）＜f（﹣1）
D.f（﹣1）＜f（）＜f（﹣ ）

【题目】已知定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=|x﹣a2|﹣a2 ，且对x∈R，恒有f（x﹣2）＜f（x），则实数a的取值范围为（）
A.
B.
C.
D.

【题目】已知函数f(x)＝4cosωx·sin(ωx＋)(ω>0)的最小正周期为π．

(1)求ω的值；

(2)讨论f(x)在区间[0，]上的单调性．

【题目】要得到y= cos2x+sinxcosx的图象，只需把y=sin2x的图象上所有点（）
A.向左平移个单位，再向上移动个单位
B.向左平移个单位，再向上移动个单位
C.向右平移个单位，再向下移动个单位
D.向右平移个单位，再向下移动个单位

【题目】已知定义在R上的函数y=f（x）的导函数为f′（x），满足f′（x）＜f（x），且f（0）=1，则不等式f（x）＜ex的解集为（）
A.（﹣∞，e4）
B.（e4 ， +∞）
C.（﹣∞，0）
D.（0，+∞）

【题目】已知函数f（x）=x2﹣2lnx．
（1）求证：f（x）在（1，+∞）上单调递增．
（2）若f（x）≥2tx﹣ 在x∈（0，1]内恒成立，求实数t的取值范围．

【题目】对于函数f（x）= ，有下列5个结论： ①任取x1 ， x2∈[0，+∞），都有|f（x1）﹣f（x2）|≤2；
②函数y=f（x）在区间[4，5]上单调递增；
③f（x）=2kf（x+2k）（k∈N+），对一切x∈[0，+∞）恒成立；
④函数y=f（x）﹣ln（x﹣1）有3个零点；
⑤若关于x的方程f（x）=m（m＜0）有且只有两个不同实根x1 ， x2 ，则x1+x2=3．
则其中所有正确结论的序号是．（请写出全部正确结论的序号）

【题目】已知函数f（x）=sin（πx+ ）和函数g（x）=cos（πx+ ）在区间[﹣ ， ]上的图象交于A，B，C三点，则△ABC的面积是（）
A.
B.
C.
D.

试题分类