题目内容
在抛物线 y2=4x上恒有两点关于直线l:y=kx+3对称,求k的范围.
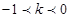
试题分析:设B,C关于直线
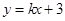 对称,根据直线垂直斜率之积等于
对称,根据直线垂直斜率之积等于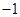 ,可知直线AB的斜率为
,可知直线AB的斜率为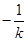 ,但这样就会有一个弊端,也就是当直线l斜率为0时,直线AB的斜率就不存在了,所以这时就需要讨论。为了省去讨论的麻烦可直接将直线AB方程设为
,但这样就会有一个弊端,也就是当直线l斜率为0时,直线AB的斜率就不存在了,所以这时就需要讨论。为了省去讨论的麻烦可直接将直线AB方程设为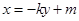 ,设出B,C坐标可得出中点M的坐标,由对称性可知中点M恒在直线l上,代入方程得到方程
,设出B,C坐标可得出中点M的坐标,由对称性可知中点M恒在直线l上,代入方程得到方程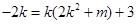 ,用k表示出m,还是有对称性可知中点M恒在抛物线内部,得到不等式
,用k表示出m,还是有对称性可知中点M恒在抛物线内部,得到不等式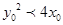 ,代入
,代入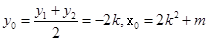 代入即可得出k的范围。
代入即可得出k的范围。试题解析:设B,C关于直线
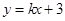 对称,直线BC方程为
对称,直线BC方程为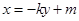 ,代入y2=4x,得
,代入y2=4x,得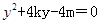 。设
。设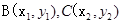 ,B,C中点
,B,C中点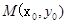 ,所以
,所以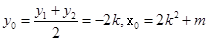 ,因为
,因为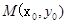 在直线
在直线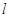 上,所以
上,所以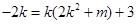 ,整理得
,整理得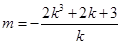 ,因为
,因为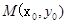 在抛物线y2=4x内部,则
在抛物线y2=4x内部,则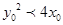 ,把m代入化简得
,把m代入化简得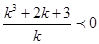 ,即
,即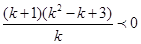 ,解得
,解得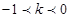

练习册系列答案
相关题目
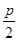 (p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.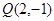 ,F为抛物线
,F为抛物线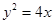 的焦点,动点
的焦点,动点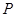 为抛物线上任意一点,当
为抛物线上任意一点,当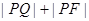 取最小值时P的坐标为________.
取最小值时P的坐标为________.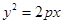
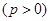 ,过其焦点且斜率为-1的直线交抛物线于
,过其焦点且斜率为-1的直线交抛物线于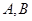 两点,若线段
两点,若线段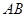 的中点的纵坐标为-2,则该抛物线的准线方程为( )
的中点的纵坐标为-2,则该抛物线的准线方程为( )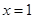
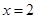
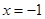
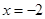
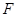 是抛物线
是抛物线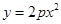
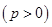 的焦点,
的焦点,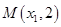 、
、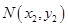 、
、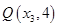 是这条抛物线上的三点,且
是这条抛物线上的三点,且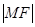 、
、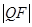 、
、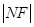 成等差数列.则
成等差数列.则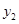 的值是( )
的值是( )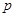 的值有关
的值有关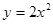 上两点
上两点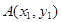 、
、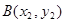 关于直线
关于直线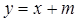 对称,且
对称,且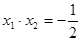 ,则
,则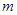 等于( )
等于( )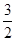
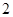
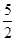
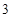
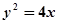 与双曲线
与双曲线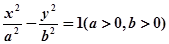 有相同的焦点F,点
有相同的焦点F,点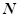 是两曲线的交点,且
是两曲线的交点,且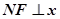 轴,则
轴,则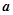 的值为( )
的值为( )
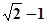
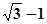

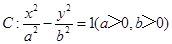 与抛物线
与抛物线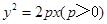 相交于A,B两点,公共弦AB恰好过它们的公共焦点F,则双曲线C的离心率为( )
相交于A,B两点,公共弦AB恰好过它们的公共焦点F,则双曲线C的离心率为( )