题目内容
已知直线l1:4x-3y+6=0和直线l2:x=-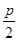 (p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(1)求抛物线C的方程;
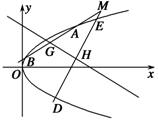
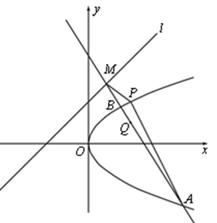
(2)若拋物线上任意一点M处的切线l与直线l2交于点N,试问在x轴上是否存在定点Q,使Q点在以MN为直径的圆上,若存在,求出点Q的坐标;若不存在,请说明理由.
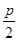 (p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.(1)求抛物线C的方程;
(2)若拋物线上任意一点M处的切线l与直线l2交于点N,试问在x轴上是否存在定点Q,使Q点在以MN为直径的圆上,若存在,求出点Q的坐标;若不存在,请说明理由.
(1)y2=4x(2)存在定点Q(1,0),使Q在以MN为直径的圆上.
(1)由定义知l2为抛物线的准线,抛物线焦点F ,由抛物线定义知抛物线上点到直线l2的距离等于其到焦点F的距离.
,由抛物线定义知抛物线上点到直线l2的距离等于其到焦点F的距离.
所以抛物线上的点到直线l1和直线l2的距离之和的最小值为焦点F到直线l1的距离.
所以2= ,则p=2,所以抛物线方程为y2=4x.
,则p=2,所以抛物线方程为y2=4x.
(2)设M(x0,y0),由题意知直线斜率存在,设为k,且k≠0,所以直线l方程为y-y0=k(x-x0),
代入y2=4x消x得ky2-4y+4y0-k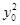 =0.
=0.
由Δ=16-4k(4y0-k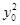 )=0,得k=
)=0,得k= .
.
所以直线l方程为y-y0= (x-x0),
(x-x0),
令x=-1,又由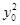 =4x0,得N
=4x0,得N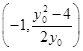 .
.
设Q(x1,0)则 =(x0-x1,y0),
=(x0-x1,y0), =
= .
.
由题意知 ·
· =0,即(x0-x1)(-1-x1)+
=0,即(x0-x1)(-1-x1)+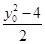 =0,把
=0,把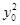 =4x0代入,得(1-x1)x0+
=4x0代入,得(1-x1)x0+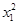 +x1-2=0,因为对任意的x0等式恒成立,所以
+x1-2=0,因为对任意的x0等式恒成立,所以
所以x1=1,即在x轴上存在定点Q(1,0),使Q在以MN为直径的圆上.
 ,由抛物线定义知抛物线上点到直线l2的距离等于其到焦点F的距离.
,由抛物线定义知抛物线上点到直线l2的距离等于其到焦点F的距离.所以抛物线上的点到直线l1和直线l2的距离之和的最小值为焦点F到直线l1的距离.
所以2=
 ,则p=2,所以抛物线方程为y2=4x.
,则p=2,所以抛物线方程为y2=4x.(2)设M(x0,y0),由题意知直线斜率存在,设为k,且k≠0,所以直线l方程为y-y0=k(x-x0),
代入y2=4x消x得ky2-4y+4y0-k
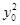 =0.
=0.由Δ=16-4k(4y0-k
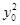 )=0,得k=
)=0,得k= .
.所以直线l方程为y-y0=
 (x-x0),
(x-x0),令x=-1,又由
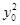 =4x0,得N
=4x0,得N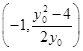 .
.设Q(x1,0)则
 =(x0-x1,y0),
=(x0-x1,y0), =
= .
.由题意知
 ·
· =0,即(x0-x1)(-1-x1)+
=0,即(x0-x1)(-1-x1)+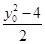 =0,把
=0,把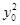 =4x0代入,得(1-x1)x0+
=4x0代入,得(1-x1)x0+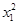 +x1-2=0,因为对任意的x0等式恒成立,所以
+x1-2=0,因为对任意的x0等式恒成立,所以
所以x1=1,即在x轴上存在定点Q(1,0),使Q在以MN为直径的圆上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
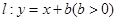 ,抛物线
,抛物线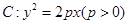 ,已知点
,已知点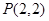 在抛物线
在抛物线 上,且抛物线
上,且抛物线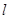 的距离的最小值为
的距离的最小值为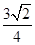 .
.
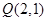 的任一直线(不经过点
的任一直线(不经过点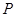 )与抛物线
)与抛物线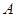 、
、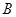 两点,直线
两点,直线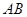 与直线
与直线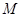 ,记直线
,记直线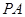 ,
,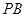 ,
,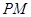 的斜率分别为
的斜率分别为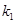 ,
,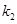 ,
, 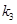 .问:是否存在实数
.问:是否存在实数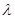 ,使得
,使得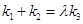 ?若存在,试求出
?若存在,试求出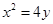 ,下列描述正确的是
,下列描述正确的是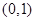
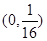
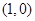
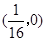
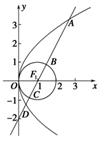
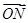 =
=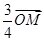 ,O为坐标原点.
,O为坐标原点.