题目内容
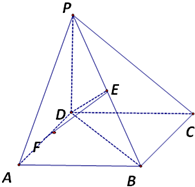
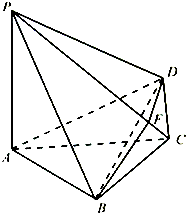
如图,四棱锥P-ABCD中,PA⊥底面ABCD,PA=2
,BC=CD=2,∠ACB=∠ACD=
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若侧棱PC上的点F满足PF=7FC,求三棱锥P-BDF的体积.
| 3 |
| π |
| 3 |
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若侧棱PC上的点F满足PF=7FC,求三棱锥P-BDF的体积.

(Ⅰ)∵BC=CD=2,∴△BCD为等腰三角形,再由 ∠ACB=∠ACD=
,∴BD⊥AC.
再由PA⊥底面ABCD,可得PA⊥BD.
而PA∩AC=A,故BD⊥平面PAC.
(Ⅱ)∵侧棱PC上的点F满足PF=7FC,
∴三棱锥F-BCD的高是三棱锥P-BCD的高的
.
△BCD的面积S△BCD=
BC•CD•sin∠BCD=
×2×2×sin
=
.
∴三棱锥P-BDF的体积 V=VP-BCD-VF-BCD=
•S△BCD•PA-
•S△BCD•
•PA=
×
•S△BCD•PA
=
×
×2
=
.
| π |
| 3 |
再由PA⊥底面ABCD,可得PA⊥BD.
而PA∩AC=A,故BD⊥平面PAC.
(Ⅱ)∵侧棱PC上的点F满足PF=7FC,
∴三棱锥F-BCD的高是三棱锥P-BCD的高的
| 1 |
| 8 |
△BCD的面积S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 3 |
∴三棱锥P-BDF的体积 V=VP-BCD-VF-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 8 |
| 7 |
| 8 |
| 1 |
| 3 |
=
| 7 |
| 24 |
| 3 |
| 3 |
| 7 |
| 4 |

练习册系列答案
相关题目