Question

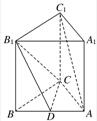
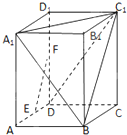
在长方体ABCD-A₁B₁C₁D₁中，E，F分别是AD，DD₁的中点，AB=BC=2，A₁A=2

2

（Ⅰ）求证：EF∥平面A₁BC₁；
（Ⅱ）在线段BC₁是否存在点P，使直线A₁P与C₁D垂直，如果存在，求线段A₁P的长，如果不存在，请说明理由．

Answer 1

证明：（Ⅰ）连接AD₁，在长方体ABCD-A₁B₁C₁D₁中，
AB

∥ .

.

D1C1，则四边形ABC₁D₁是平行四边形，
∴AD₁∥BC₁，
又∵E，F分别是AD，DD₁的中点
∴AD₁∥EF，
∴EF∥BC₁，又EF?面A₁BC₁，BC₁?面A₁BC₁，
∴EF∥平面A₁BC₁（3分）
（II）在平面CC₁D₁D中作D₁Q⊥C₁D交CC₁于Q，
过Q作QP∥CB交BC₁于点P，则A₁P⊥C₁D．（7分）
因为A₁D₁⊥平面CC₁D₁D，C₁D?平面CC₁D₁D，
∴C₁D⊥A₁D₁，而QP∥CB，CB∥A₁D₁，∴QP∥A₁D₁，
又∵A₁D₁∩D₁Q=D₁，∴C₁D⊥平面A₁PQC₁，
且A₁P?平面A₁PQC₁，∴A₁P⊥C₁D．（10分）
∵△D₁C₁Q∽Rt△C₁CD，
∴

C1Q

CD

=

D1C1

C1C

，∴C1Q=

2

又∵PQ∥BC，
∴PQ=

1

2

BC=1．
∵四边形A₁PQD₁为直角梯形，且高D1Q=

6

，
∴A1P=

(2-1)2+6

=

7

．（14分）