题目内容
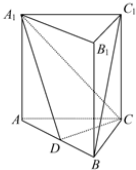
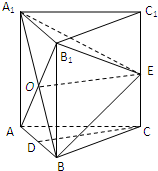
如图,在三棱柱ABC-A1B1C1中,每个侧面均为正方形,D为底边AB的中点,E为侧棱CC1的中点,AB1与A1B的交点为O.
(1)求证:CD∥平面A1EB;
(2)求证:AB1⊥平面A1EB.
(1)求证:CD∥平面A1EB;
(2)求证:AB1⊥平面A1EB.

证明:(1)设AB1和A1B的交点为O,连接EO,连接OD.
因为O为AB1的中点,D为AB的中点,所以OD∥BB1且OD=
BB1.
又E是CC1中点,
则EC∥BB1且EC=
BB1,即EC∥OD且EC=OD,
则四边形ECOD为平行四边形.所以EO∥CD.
又CD?平面A1BE,EO?平面A1BE,
则CD∥平面A1BE.…(7分)
(2)因为三棱柱各侧面都是正方形,所以BB1⊥AB,BB1⊥BC,
所以BB1⊥平面ABC.
因为CD?平面ABC,所以BB1⊥CD.
由已知得AB=BC=AC,所以CD⊥AB.
所以CD⊥平面A1ABB1.
由(1)可知EO∥CD,所以EO⊥平面A1ABB1.
所以EO⊥AB1.
因为侧面是正方形,所以AB1⊥A1B.
又EO∩A1B=O,EO?平面A1EB,A1B?平面A1EB,
所以AB1⊥平面A1BE.…(14分)

因为O为AB1的中点,D为AB的中点,所以OD∥BB1且OD=
| 1 |
| 2 |
又E是CC1中点,
则EC∥BB1且EC=
| 1 |
| 2 |
则四边形ECOD为平行四边形.所以EO∥CD.
又CD?平面A1BE,EO?平面A1BE,
则CD∥平面A1BE.…(7分)
(2)因为三棱柱各侧面都是正方形,所以BB1⊥AB,BB1⊥BC,
所以BB1⊥平面ABC.
因为CD?平面ABC,所以BB1⊥CD.
由已知得AB=BC=AC,所以CD⊥AB.
所以CD⊥平面A1ABB1.
由(1)可知EO∥CD,所以EO⊥平面A1ABB1.
所以EO⊥AB1.
因为侧面是正方形,所以AB1⊥A1B.
又EO∩A1B=O,EO?平面A1EB,A1B?平面A1EB,
所以AB1⊥平面A1BE.…(14分)


练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目