题目内容
对于椭圆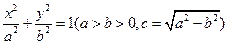 ,定义
,定义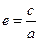 为椭圆的离心率,椭圆离心率的取值范围是
为椭圆的离心率,椭圆离心率的取值范围是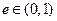 ,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆
,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆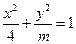 与椭圆
与椭圆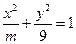 相似,则
相似,则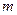 的值为
的值为
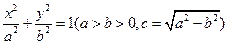 ,定义
,定义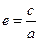 为椭圆的离心率,椭圆离心率的取值范围是
为椭圆的离心率,椭圆离心率的取值范围是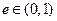 ,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆
,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆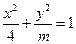 与椭圆
与椭圆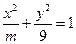 相似,则
相似,则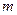 的值为
的值为 6
略

练习册系列答案
相关题目
题目内容
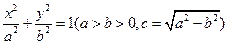 ,定义
,定义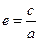 为椭圆的离心率,椭圆离心率的取值范围是
为椭圆的离心率,椭圆离心率的取值范围是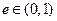 ,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆
,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆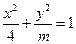 与椭圆
与椭圆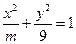 相似,则
相似,则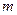 的值为
的值为 