题目内容
(本小题满分12分)
如图,在直角坐标系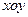 中,已知椭圆
中,已知椭圆 :
: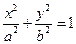
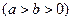 的离心率
的离心率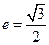 ,左、右两个焦点分别为
,左、右两个焦点分别为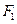 、
、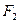 。过右焦点
。过右焦点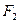 且与
且与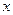 轴垂直的直线与椭圆
轴垂直的直线与椭圆 相交
相交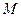 、
、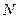 两点,且
两点,且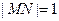 .
.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左顶点为
的左顶点为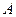 ,下顶点为
,下顶点为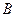 ,动点
,动点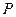 满足
满足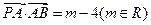 ,试求点
,试求点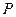 的轨迹方程,使点
的轨迹方程,使点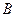 关于该轨迹的对称点落在椭圆
关于该轨迹的对称点落在椭圆 上.
上.
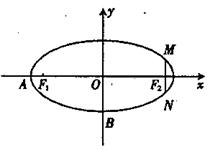
如图,在直角坐标系
 中,已知椭圆
中,已知椭圆 :
: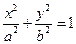
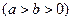 的离心率
的离心率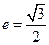 ,左、右两个焦点分别为
,左、右两个焦点分别为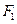 、
、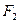 。过右焦点
。过右焦点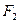 且与
且与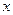 轴垂直的直线与椭圆
轴垂直的直线与椭圆 相交
相交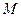 、
、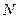 两点,且
两点,且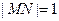 .
.(1)求椭圆
 的方程;
的方程;(2)设椭圆
 的左顶点为
的左顶点为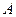 ,下顶点为
,下顶点为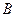 ,动点
,动点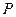 满足
满足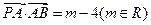 ,试求点
,试求点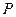 的轨迹方程,使点
的轨迹方程,使点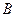 关于该轨迹的对称点落在椭圆
关于该轨迹的对称点落在椭圆 上.
上.
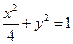 ,P的轨迹方程为
,P的轨迹方程为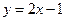 或
或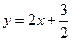
(1)∵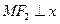 轴,∴
轴,∴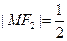 ,由椭圆的定义得:
,由椭圆的定义得: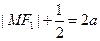
∵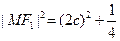 ,∴
,∴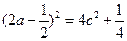 ……………………2分
……………………2分
又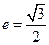 得
得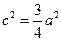 ,∴
,∴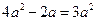 ,∵
,∵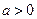 ,∴
,∴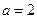 ,
,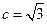 ,
,
∴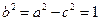 ,
,
∴所求椭圆 的方程为
的方程为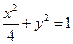 ……………………5分
……………………5分
(2)由(1)知点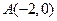 ,点
,点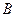 为
为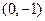 ,设点
,设点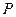 的坐标为
的坐标为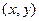 ,
,
则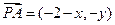 ,
,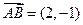 ,
,
由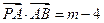 得
得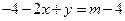 ,
,
∴点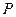 的轨迹方程为
的轨迹方程为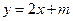 ……………………7分
……………………7分
设点B关于P的轨迹的对称点为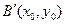 ,则由轴对称的性质可得
,则由轴对称的性质可得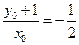 ,
,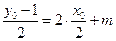 ,解得
,解得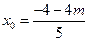 ,
,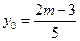 ……………………9分
……………………9分
∵点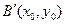 在椭圆上,∴
在椭圆上,∴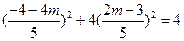 ,整理得
,整理得
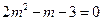 ,解得
,解得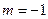 或
或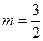 。
。
∴点P的轨迹方程为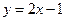 或
或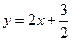 ,……………………11分
,……………………11分
经检验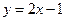 和
和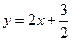 都符合题设,
都符合题设,
∴满足条件的点P的轨迹方程为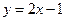 或
或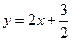 ……………………12分
……………………12分
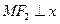 轴,∴
轴,∴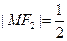 ,由椭圆的定义得:
,由椭圆的定义得: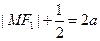
∵
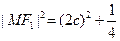 ,∴
,∴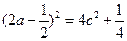 ……………………2分
……………………2分又
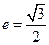 得
得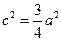 ,∴
,∴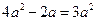 ,∵
,∵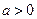 ,∴
,∴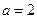 ,
,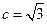 ,
,∴
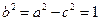 ,
,∴所求椭圆
 的方程为
的方程为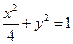 ……………………5分
……………………5分(2)由(1)知点
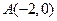 ,点
,点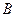 为
为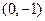 ,设点
,设点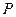 的坐标为
的坐标为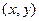 ,
,则
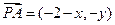 ,
,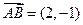 ,
,由
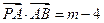 得
得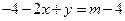 ,
,∴点
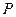 的轨迹方程为
的轨迹方程为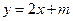 ……………………7分
……………………7分设点B关于P的轨迹的对称点为
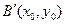 ,则由轴对称的性质可得
,则由轴对称的性质可得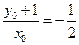 ,
,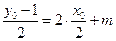 ,解得
,解得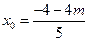 ,
,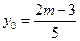 ……………………9分
……………………9分∵点
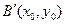 在椭圆上,∴
在椭圆上,∴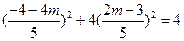 ,整理得
,整理得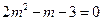 ,解得
,解得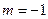 或
或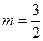 。
。∴点P的轨迹方程为
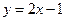 或
或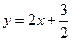 ,……………………11分
,……………………11分经检验
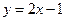 和
和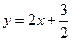 都符合题设,
都符合题设,∴满足条件的点P的轨迹方程为
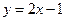 或
或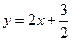 ……………………12分
……………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
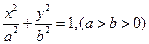 ,其相应于焦点
,其相应于焦点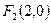 的准线方程为
的准线方程为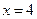 。
。 (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;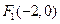 倾斜角为
倾斜角为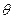 的直线分别交椭圆C于A、B两点,求证:
的直线分别交椭圆C于A、B两点,求证: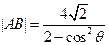 ;
;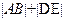 的最小值。
的最小值。 :
: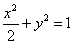 的左、右焦点分别为
的左、右焦点分别为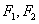 ,下顶点为
,下顶点为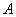 ,点
,点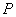 是椭圆上任一点,⊙
是椭圆上任一点,⊙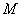 是以
是以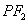 为直径的圆.
为直径的圆.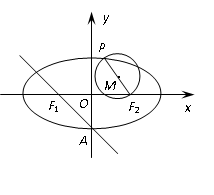
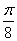 时,求
时,求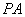 所在直线的方程;
所在直线的方程;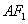 相切时,求⊙
相切时,求⊙ 椭圆
椭圆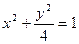 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线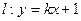 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。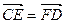 ,求直线
,求直线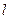 的方程;
的方程;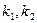 ,若
,若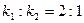 ,求k的值。
,求k的值。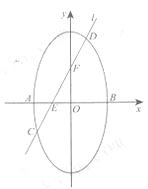
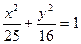 上的点,若F1、F2是椭圆的两个焦点,则
上的点,若F1、F2是椭圆的两个焦点,则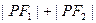 等于
等于 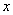 轴上,左右焦点分别为
轴上,左右焦点分别为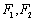 ,且
,且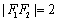 ,点(1,
,点(1,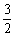 )在椭圆C上.
)在椭圆C上.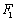 的直线
的直线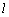 与椭圆
与椭圆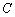 相交于
相交于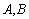 两点,且
两点,且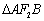 的面积为
的面积为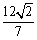 ,求以
,求以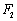 为圆心且与直线
为圆心且与直线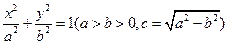 ,定义
,定义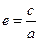 为椭圆的离心率,椭圆离心率的取值范围是
为椭圆的离心率,椭圆离心率的取值范围是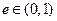 ,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆
,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆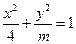 与椭圆
与椭圆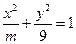 相似,则
相似,则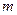 的值为
的值为 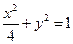 的焦点为
的焦点为 ,若点P在椭圆上,且满足
,若点P在椭圆上,且满足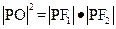 (其中
(其中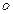 为坐标原点),则称点P为“★点”,那么下列结论正确的是 ( )
为坐标原点),则称点P为“★点”,那么下列结论正确的是 ( ) 为椭圆的左焦点,
为椭圆的左焦点, 、
、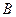 分别为椭圆的右顶点和上顶点,
分别为椭圆的右顶点和上顶点,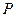 为椭圆上的点,当
为椭圆上的点,当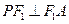 ,
,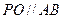 (
(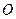 为椭圆的中心)时,椭圆的离心率为 .
为椭圆的中心)时,椭圆的离心率为 .