题目内容
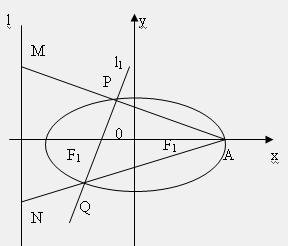
已知椭圆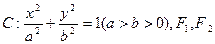 为其左、右焦点,A为右顶点,l为左准线
为其左、右焦点,A为右顶点,l为左准线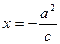 ,过
,过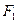 的直线
的直线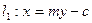 与椭圆相交于P,Q两点,且有
与椭圆相交于P,Q两点,且有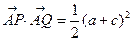

(1)求椭圆C的离心率e的最小值;
(2)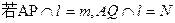 ,求证:M,N两点的纵坐标之积是定值。
,求证:M,N两点的纵坐标之积是定值。
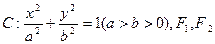 为其左、右焦点,A为右顶点,l为左准线
为其左、右焦点,A为右顶点,l为左准线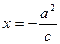 ,过
,过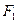 的直线
的直线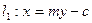 与椭圆相交于P,Q两点,且有
与椭圆相交于P,Q两点,且有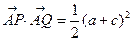

(1)求椭圆C的离心率e的最小值;

(2)
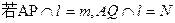 ,求证:M,N两点的纵坐标之积是定值。
,求证:M,N两点的纵坐标之积是定值。(1)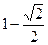 ;(2)略
;(2)略
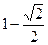 ;(2)略
;(2)略联立方程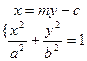 ,消去
,消去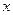 ,化简得
,化简得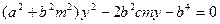 .
.
设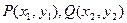 ,则有
,则有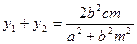 ,
,
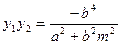
 ,
,
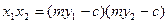
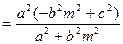 ,
,
又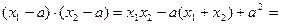
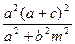
又 ,
,
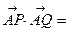
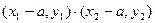
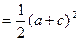 ,即
,即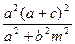
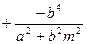
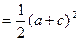
化简可得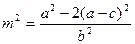 .
.
(1)由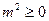 ,可得到
,可得到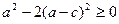 .即
.即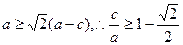 .
.
椭圆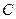 的离心率
的离心率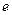 的最小值为
的最小值为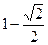 .
.
(2)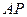 的方程为
的方程为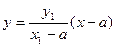 ,与
,与 的方程:
的方程: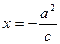 联立可得
联立可得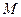 点的纵坐标为
点的纵坐标为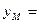
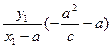 ,同理可得
,同理可得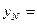
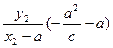 .
.
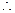
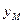
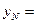

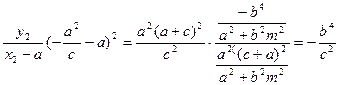 (定值)
(定值)
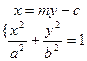 ,消去
,消去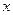 ,化简得
,化简得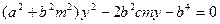 .
.
设
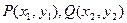 ,则有
,则有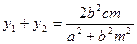 ,
,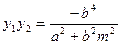
 ,
,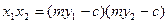
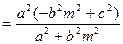 ,
, 又
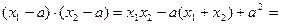
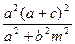
又
 ,
,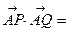
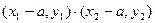
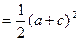 ,即
,即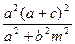
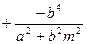
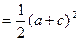
化简可得
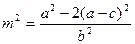 .
.(1)由
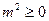 ,可得到
,可得到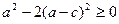 .即
.即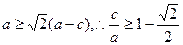 .
.椭圆
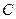 的离心率
的离心率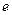 的最小值为
的最小值为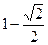 .
.(2)
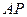 的方程为
的方程为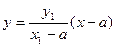 ,与
,与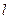 的方程:
的方程: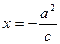 联立可得
联立可得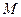 点的纵坐标为
点的纵坐标为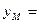
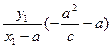 ,同理可得
,同理可得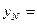
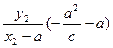 .
.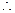
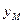
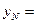

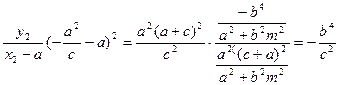 (定值)
(定值)
练习册系列答案
相关题目
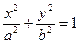 (
(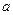 >
>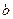 >0)上一点
>0)上一点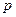 (3,4),若
(3,4),若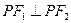 ,求椭圆方程。
,求椭圆方程。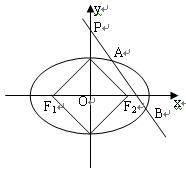
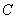 :
: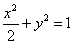 的左、右焦点分别为
的左、右焦点分别为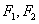 ,下顶点为
,下顶点为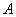 ,点
,点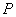 是椭圆上任一点,⊙
是椭圆上任一点,⊙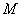 是以
是以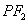 为直径的圆.
为直径的圆.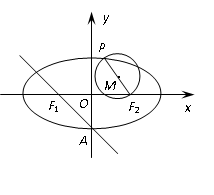
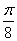 时,求
时,求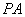 所在直线的方程;
所在直线的方程;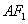 相切时,求⊙
相切时,求⊙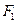 ,
,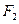 分别是椭圆
分别是椭圆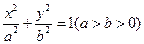 的左、右焦点,与直线
的左、右焦点,与直线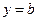 相切的
相切的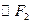 交椭圆于点
交椭圆于点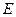 ,
,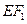 与
与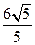 ,过椭圆的上顶点A的直线与
,过椭圆的上顶点A的直线与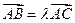 ,求λ的取值范围.
,求λ的取值范围.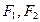 分别是椭圆
分别是椭圆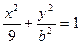
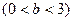 的左右焦点,若在其右准线上存在点
的左右焦点,若在其右准线上存在点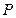
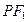 的垂直平分线恰好经过
的垂直平分线恰好经过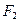 ,求
,求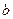 的取值范围
的取值范围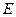 经过点
经过点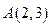 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点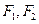 在
在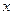 轴上,离心率
轴上,离心率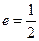 。
。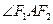 的角平分线所在直线的方程。
的角平分线所在直线的方程。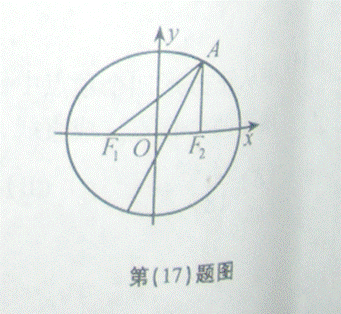
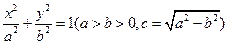 ,定义
,定义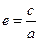 为椭圆的离心率,椭圆离心率的取值范围是
为椭圆的离心率,椭圆离心率的取值范围是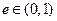 ,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆
,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆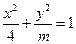 与椭圆
与椭圆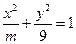 相似,则
相似,则 的值为
的值为 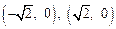 ,则PC·PD的最大值为 ( )
,则PC·PD的最大值为 ( )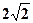 C 3 D
C 3 D