题目内容
直线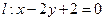 过椭圆的左焦点
过椭圆的左焦点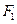 和一个顶点
和一个顶点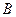 ,该椭圆的离心率为
,该椭圆的离心率为
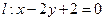 过椭圆的左焦点
过椭圆的左焦点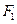 和一个顶点
和一个顶点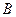 ,该椭圆的离心率为
,该椭圆的离心率为A.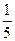 | B.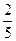 | C.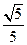 | D.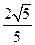 |
D
左焦点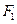 和顶点
和顶点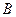 的坐标分别是(
的坐标分别是(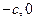 ),(
),(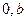 ),都在直线
),都在直线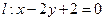 上,所以
上,所以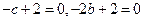 ,所以
,所以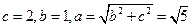 ,
,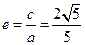 .
.
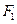 和顶点
和顶点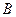 的坐标分别是(
的坐标分别是(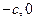 ),(
),(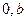 ),都在直线
),都在直线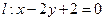 上,所以
上,所以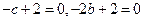 ,所以
,所以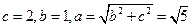 ,
,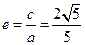 .
.
练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
题目内容
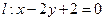 过椭圆的左焦点
过椭圆的左焦点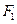 和一个顶点
和一个顶点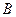 ,该椭圆的离心率为
,该椭圆的离心率为A.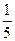 | B.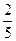 | C.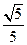 | D.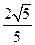 |
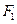 和顶点
和顶点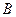 的坐标分别是(
的坐标分别是(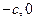 ),(
),(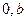 ),都在直线
),都在直线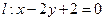 上,所以
上,所以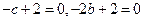 ,所以
,所以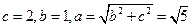 ,
,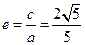 .
.
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案