题目内容
已知中心在坐标原点,焦点在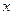 轴上的椭圆经过点M(1,
轴上的椭圆经过点M(1,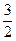 ),斜率为
),斜率为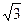 的直线经过椭圆的下顶点D和右焦点F,A、B为椭圆上不同于M的两点。
的直线经过椭圆的下顶点D和右焦点F,A、B为椭圆上不同于M的两点。
(1)求椭圆的标准方程;
(2)若直线AB过点F且不与坐标轴垂直,求线段AB的中垂线与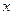 轴的交点的横坐标的取值范围。
轴的交点的横坐标的取值范围。
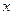 轴上的椭圆经过点M(1,
轴上的椭圆经过点M(1,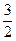 ),斜率为
),斜率为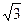 的直线经过椭圆的下顶点D和右焦点F,A、B为椭圆上不同于M的两点。
的直线经过椭圆的下顶点D和右焦点F,A、B为椭圆上不同于M的两点。(1)求椭圆的标准方程;
(2)若直线AB过点F且不与坐标轴垂直,求线段AB的中垂线与
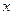 轴的交点的横坐标的取值范围。
轴的交点的横坐标的取值范围。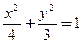 (0,
(0,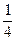 )
)、解:(1)根据题意,设椭圆的方程为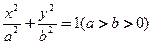 ,半焦距为
,半焦距为 ,则D(0,
,则D(0,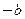 ),F(
),F( ,0),
,0),
因为直线DF的斜率为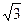 ,所以
,所以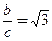 ,①
,①
因为M(1,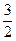 )在椭圆上,所以
)在椭圆上,所以 ,②
,②
又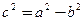 ,③由①②③得:
,③由①②③得:
所以椭圆的标准方程为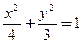
(2)设直线AB的方程为 ,代入
,代入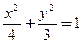 ,
,
得 ,
,
设A( ),B(
),B( ),AB为中点N(
),AB为中点N( ),
),
则 ,
,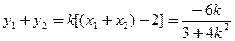 ,
,
∴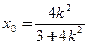 ,
, ,
,
∴AB的中垂线方程为
 ,
,
令 ,得
,得
 ,
,
又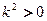 ,∴
,∴ ,
,
∴线段AB的中垂线与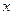 轴的交点的横坐标的取值范围是(0,
轴的交点的横坐标的取值范围是(0,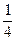 )。
)。
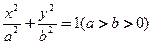 ,半焦距为
,半焦距为 ,则D(0,
,则D(0,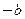 ),F(
),F( ,0),
,0),因为直线DF的斜率为
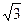 ,所以
,所以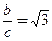 ,①
,①因为M(1,
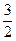 )在椭圆上,所以
)在椭圆上,所以 ,②
,②又
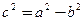 ,③由①②③得:
,③由①②③得:
所以椭圆的标准方程为
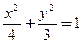
(2)设直线AB的方程为
 ,代入
,代入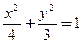 ,
,得
 ,
,设A(
 ),B(
),B( ),AB为中点N(
),AB为中点N( ),
),则
 ,
,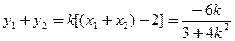 ,
,∴
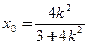 ,
, ,
,∴AB的中垂线方程为

 ,
,令
 ,得
,得
 ,
,又
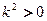 ,∴
,∴ ,
,∴线段AB的中垂线与
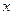 轴的交点的横坐标的取值范围是(0,
轴的交点的横坐标的取值范围是(0,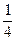 )。
)。
练习册系列答案
相关题目
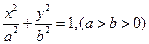 ,其相应于焦点
,其相应于焦点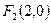 的准线方程为
的准线方程为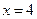 。
。 (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;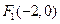 倾斜角为
倾斜角为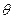 的直线分别交椭圆C于A、B两点,求证:
的直线分别交椭圆C于A、B两点,求证: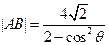 ;
;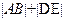 的最小值。
的最小值。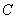 :
: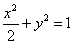 的左、右焦点分别为
的左、右焦点分别为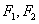 ,下顶点为
,下顶点为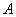 ,点
,点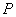 是椭圆上任一点,⊙
是椭圆上任一点,⊙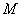 是以
是以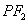 为直径的圆.
为直径的圆.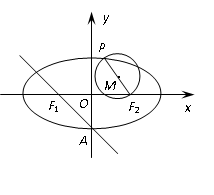
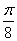 时,求
时,求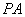 所在直线的方程;
所在直线的方程;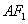 相切时,求⊙
相切时,求⊙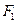 ,
,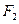 分别是椭圆
分别是椭圆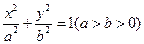 的左、右焦点,与直线
的左、右焦点,与直线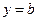 相切的
相切的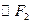 交椭圆于点
交椭圆于点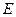 ,
,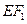 与
与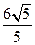 ,过椭圆的上顶点A的直线与
,过椭圆的上顶点A的直线与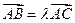 ,求λ的取值范围.
,求λ的取值范围. 椭圆
椭圆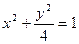 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线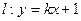 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。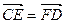 ,求直线
,求直线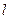 的方程;
的方程;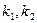 ,若
,若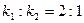 ,求k的值。
,求k的值。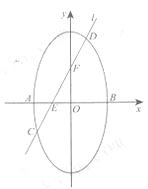
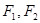 是椭圆
是椭圆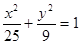 的两个焦点,
的两个焦点,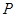 是椭圆上的任意一点,则
是椭圆上的任意一点,则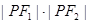 的最大值是 ( )
的最大值是 ( )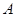 、9
、9 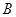 、16
、16 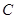 、
、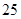
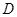 、
、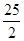
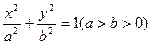 的离心率为
的离心率为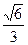 ,长轴长为
,长轴长为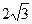 ,直线
,直线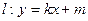 交椭圆于不同的两点A、B。
交椭圆于不同的两点A、B。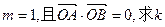 的值(O点为坐标原点);
的值(O点为坐标原点);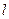 的距离为
的距离为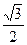 ,求
,求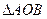 面积的最大值。
面积的最大值。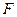 是椭圆
是椭圆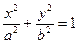 (a>b>0)的左焦点,直线
(a>b>0)的左焦点,直线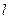 为对应的准线,直线
为对应的准线,直线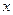 轴
轴 
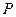 点,
点, 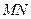 为椭圆的长轴,已知
为椭圆的长轴,已知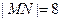 ,且
,且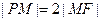 .
.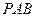 ,恒有
,恒有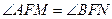 ;
;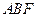 面积的最大值.
面积的最大值.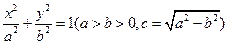 ,定义
,定义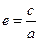 为椭圆的离心率,椭圆离心率的取值范围是
为椭圆的离心率,椭圆离心率的取值范围是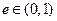 ,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆
,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆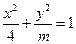 与椭圆
与椭圆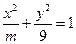 相似,则
相似,则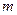 的值为
的值为