题目内容
8.设m,n为空间两条不同的直线,α,β为空间两个不同的平面,给出下列命题:①若m∥α,m∥β,则α∥β;
②若m∥α,m∥n则n∥α;
③若m⊥α,m∥β,则α⊥β;
④若m⊥α,α∥β,则m⊥β.
其中的正确命题序号是( )
| A. | ③④ | B. | ②④ | C. | ①② | D. | ①③ |
分析 利用空间线面平行、线面垂直的性质定理和判定定理分别分析四个命题,得到正确答案.
解答 解:对于①,若m∥α,m∥β,则α与β可能相交;故①错误;
对于②,若m∥α,m∥n则n可能在α内;故②错误;
对于③,若m⊥α,m∥β,根据线面垂直和线面平行的性质定理以及面面垂直的判定定理得到α⊥β;故③正确;
对于④,若m⊥α,α∥β,则根据线面垂直的性质定理以及面面平行的性质定理得到m⊥β;故④正确;
故选A.
点评 本题考查了空间线面平行、线面垂直面面垂直的性质定理和判定定理的运用;熟练掌握定理是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的相关数据,如表所示.
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)求x,y的值.
(2)求顾客一次购物的结算时间超过2分钟的概率.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)求x,y的值.
(2)求顾客一次购物的结算时间超过2分钟的概率.
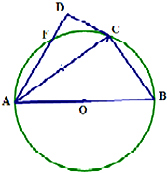 已知AB是⊙O的直径,F为圆上一点,∠BAF的角平分线与圆交于点C,过点C作圆的切线与直线AF相交于点D,若AB=6,∠DAB=$\frac{π}{3}$
已知AB是⊙O的直径,F为圆上一点,∠BAF的角平分线与圆交于点C,过点C作圆的切线与直线AF相交于点D,若AB=6,∠DAB=$\frac{π}{3}$