题目内容
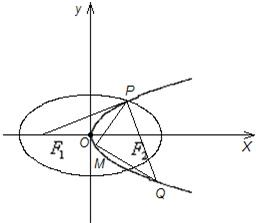
在平面直角坐标系xOy中,动点P到两点(-
,0),(
,0)的距离之和等于4,设点P的轨迹为曲线C,直线l过点E(-1,0)且与曲线C交于A,B两点.
(1)求曲线C的轨迹方程;
(2)若AB中点横坐标为-
,求直线AB的方程;
(3)是否存在△AOB面积的最大值,若存在,求出△AOB的面积;若不存在,说明理由.
| 3 |
| 3 |
(1)求曲线C的轨迹方程;
(2)若AB中点横坐标为-
| 1 |
| 2 |
(3)是否存在△AOB面积的最大值,若存在,求出△AOB的面积;若不存在,说明理由.
(1)由椭圆定义可知,点P的轨迹C是以(-
,0),(
,0)为焦点,长半轴长为2的椭圆.
故曲线C的方程为
+y2=1.
(2)设A(x1,y1),B(x2,y2),AB中点横坐标为y,则
+y12=1,
+y22=1
两方程相减可得
+(y1+y2)(y1-y2)=0
∵直线l过点E(-1,0)且与曲线C交于A,B两点,AB中点横坐标为-
,
∴
+2y(y1-y2)=0
∴
+2y•
=0
∴y=±
∴直线AB的斜率为k=±
∴直线AB的方程为y=±
(x+1);
(3)存在△AOB面积的最大值.
因为直线l过点E(-1,0),可设直线l的方程为x=my-1.
代入椭圆方程整理得(m2+4)y2-2my-3=0.
设A(x1,y1),B(x2,y2),解得y1=
,y2=
.
则|y2-y1|=
.
∴S△AOB=
|OE||y2-y1|=
设t=
(t≥
),则g(t)=
∵y=t+
在区间[
,+∞)上为增函数.
∴t+
≥
.
∴S△AOB≤
,当且仅当m=0时取等号,
∴S△AOB的最大值为
.
| 3 |
| 3 |
故曲线C的方程为
| x2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),AB中点横坐标为y,则
| x12 |
| 4 |
| x22 |
| 4 |
两方程相减可得
| (x1+x2)(x1-x2) |
| 4 |
∵直线l过点E(-1,0)且与曲线C交于A,B两点,AB中点横坐标为-
| 1 |
| 2 |
∴
| -(x1-x2) |
| 4 |
∴
| -1 |
| 4 |
| y | ||
-
|
∴y=±
| 1 |
| 4 |
∴直线AB的斜率为k=±
| 1 |
| 2 |
∴直线AB的方程为y=±
| 1 |
| 2 |
(3)存在△AOB面积的最大值.
因为直线l过点E(-1,0),可设直线l的方程为x=my-1.
代入椭圆方程整理得(m2+4)y2-2my-3=0.
设A(x1,y1),B(x2,y2),解得y1=
m+2
| ||
| m2+4 |
m-2
| ||
| m2+4 |
则|y2-y1|=
4
| ||
| m2+4 |
∴S△AOB=
| 1 |
| 2 |
2
| ||
| m2+4 |
设t=
| m2+3 |
| 3 |
| 2 | ||
t+
|
∵y=t+
| 1 |
| t |
| 3 |
∴t+
| 1 |
| t |
4
| ||
| 3 |
∴S△AOB≤
| ||
| 2 |
∴S△AOB的最大值为
| ||
| 2 |

练习册系列答案
相关题目
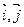 为直角坐标平面内x轴,y轴正方向上的单位向量.若向量
为直角坐标平面内x轴,y轴正方向上的单位向量.若向量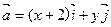 ,
,
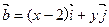 ,且
,且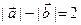 .(1)求满足上述条件的点
.(1)求满足上述条件的点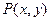 的轨迹方程;(2)设
的轨迹方程;(2)设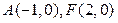 ,问是否存在常数
,问是否存在常数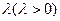 ,使得
,使得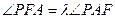 恒成立?证明你的结论.
恒成立?证明你的结论.
 (Ⅰ)建立适当的坐标系,求双曲线E的方程;
(Ⅰ)建立适当的坐标系,求双曲线E的方程;
 :
: 上一点
上一点 到其焦点的距离为
到其焦点的距离为 .
. 与
与 的值;
的值; 的横坐标为
的横坐标为 ,过
,过 ,交
,交 轴于点
轴于点 ,过点
,过点 的垂线交
的垂线交 .若
.若 是
是 的最小值.
的最小值.