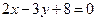题目内容
(本题满分14分)设直线 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数
. 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:


根据上图,试推测曲线 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数
. 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.(Ⅱ)观察下图:


根据上图,试推测曲线
 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.略
(Ⅰ)由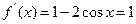 得
得 , -------1分
, -------1分
分当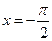 时,
时, ,此时
,此时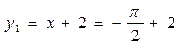 ,
,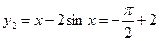 , -------2分
, -------2分
 ,所以
,所以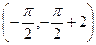 是直线
是直线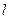 与曲线
与曲线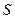 的一个切点;-------3分
的一个切点;-------3分
当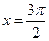 时,
时, ,此时
,此时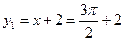 ,
,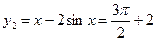 ,------4分
,------4分
 ,所以
,所以 是直线
是直线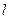 与曲线
与曲线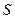 的一个切点; -----5分
的一个切点; -----5分
所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,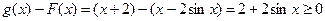 ,所以
,所以 --------6分
--------6分
因此直线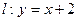 是曲线
是曲线 的“上夹线”. ----------7分
的“上夹线”. ----------7分
(Ⅱ)推测: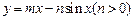 的“上夹线”的方程为
的“上夹线”的方程为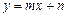 ------9分
------9分
①先检验直线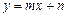 与曲线
与曲线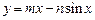 相切,且至少有两个切点:
相切,且至少有两个切点:
设: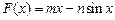
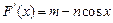 ,
,
令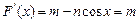 ,得:
,得: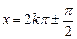 (k
(k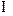 Z)-----10分
Z)-----10分
当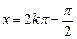 时,
时,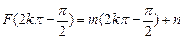
故:过曲线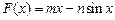 上的点(
上的点( ,
,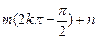 )的切线方程为:
)的切线方程为:
y-[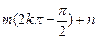 ]=
]= [
[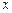 -(
-( )],化简得:
)],化简得: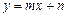 .
.
即直线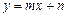 与曲线
与曲线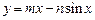 相切且有无数个切点.----12分
相切且有无数个切点.----12分
不妨设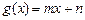 ,②下面检验g(x)
,②下面检验g(x)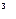 F(x)
F(x)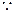 g(x)-F(x)=
g(x)-F(x)= 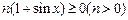
直线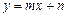 是曲线
是曲线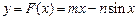 的“上夹线”.--------14分
的“上夹线”.--------14分
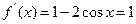 得
得 , -------1分
, -------1分分当
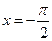 时,
时, ,此时
,此时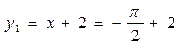 ,
,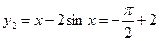 , -------2分
, -------2分 ,所以
,所以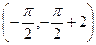 是直线
是直线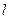 与曲线
与曲线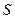 的一个切点;-------3分
的一个切点;-------3分当
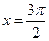 时,
时, ,此时
,此时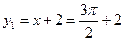 ,
,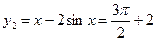 ,------4分
,------4分 ,所以
,所以 是直线
是直线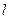 与曲线
与曲线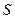 的一个切点; -----5分
的一个切点; -----5分所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,
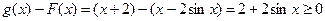 ,所以
,所以 --------6分
--------6分因此直线
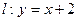 是曲线
是曲线 的“上夹线”. ----------7分
的“上夹线”. ----------7分(Ⅱ)推测:
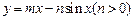 的“上夹线”的方程为
的“上夹线”的方程为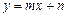 ------9分
------9分①先检验直线
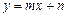 与曲线
与曲线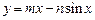 相切,且至少有两个切点:
相切,且至少有两个切点:设:
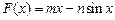
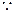
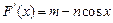 ,
,令
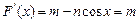 ,得:
,得: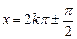 (k
(k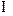 Z)-----10分
Z)-----10分当
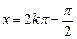 时,
时,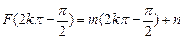
故:过曲线
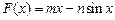 上的点(
上的点( ,
,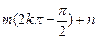 )的切线方程为:
)的切线方程为:y-[
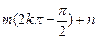 ]=
]= [
[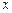 -(
-( )],化简得:
)],化简得: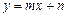 .
.即直线
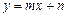 与曲线
与曲线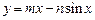 相切且有无数个切点.----12分
相切且有无数个切点.----12分不妨设
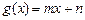 ,②下面检验g(x)
,②下面检验g(x)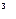 F(x)
F(x)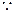 g(x)-F(x)=
g(x)-F(x)= 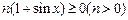
直线
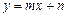 是曲线
是曲线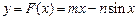 的“上夹线”.--------14分
的“上夹线”.--------14分
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
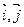 为直角坐标平面内x轴,y轴正方向上的单位向量.若向量
为直角坐标平面内x轴,y轴正方向上的单位向量.若向量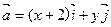 ,
,
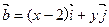 ,且
,且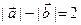 .(1)求满足上述条件的点
.(1)求满足上述条件的点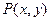 的轨迹方程;(2)设
的轨迹方程;(2)设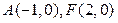 ,问是否存在常数
,问是否存在常数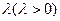 ,使得
,使得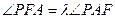 恒成立?证明你的结论.
恒成立?证明你的结论.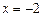 ,且直线l与x轴交于点M,圆
,且直线l与x轴交于点M,圆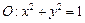 与x轴交于
与x轴交于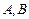 两点(如图).
两点(如图).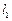 交圆于
交圆于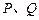 两点,且圆孤
两点,且圆孤 恰为圆周的
恰为圆周的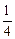 ,求直线
,求直线
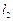 交(II)中的一个椭圆于
交(II)中的一个椭圆于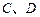 两点,其中
两点,其中 分)
分) 满足到点
满足到点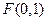 的距离比到直线
的距离比到直线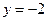 的距离小1.
的距离小1. 求曲线C的方程;
求曲线C的方程;
 过点F的直线l与曲线C交于A、B两点.(
过点F的直线l与曲线C交于A、B两点.( ⅰ)过A、B两点分别作抛物线的切线,设其交点为M,证明
ⅰ)过A、B两点分别作抛物线的切线,设其交点为M,证明 :
: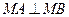 ;(ⅱ)是否在y轴上存在定点Q
;(ⅱ)是否在y轴上存在定点Q ,使得
,使得 无论AB怎样运动,都有
无论AB怎样运动,都有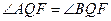 ?证明你的结论.
?证明你的结论.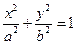 (a>b>0)相交于不同两点A、B,
(a>b>0)相交于不同两点A、B,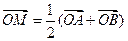 ,且
,且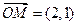 ,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,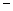 1). (I)求椭圆的离心率
1). (I)求椭圆的离心率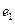 ; (II)设双曲线的离心率为
; (II)设双曲线的离心率为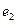 ,记
,记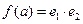 ,求
,求 的解析式,并求其定义域和值域.
的解析式,并求其定义域和值域.
 (Ⅰ)建立适当的坐标系,求双曲线E的方程;
(Ⅰ)建立适当的坐标系,求双曲线E的方程;
 :
: 上一点
上一点 到其焦点的距离为
到其焦点的距离为 .
. 与
与 的值;
的值; 的横坐标为
的横坐标为 ,过
,过 ,交
,交 轴于点
轴于点 ,过点
,过点 的垂线交
的垂线交 .若
.若 是
是 的最小值.
的最小值. 过点(-1,2)且与直线
过点(-1,2)且与直线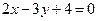 垂直,则
垂直,则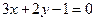 b.
b.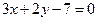
 d.
d.