Question

【题目】在边长为8正方形中，点为的中点，是上一点，且，若对于常数，在正方形的边上恰有个不同的点，使得，则实数的取值范围为______.

Answer 1

【答案】

【解析】

建立平面直角坐标系，按照点P在线段，，，上进行逐段分析的取值范围及对应的解，然后取各个范围的交集即可得答案．

以AB所在直线为x轴，以AD所在直线为y轴建立平面直角坐标系，如图所示，

则，，

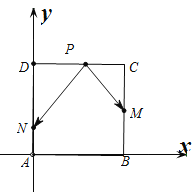
（1）当点P在AB上时，设，，

∴，，

∴，

∵，

∴．

∴当时有一解，当时有两解；

（2）当点P在AD上时，设，，

∴，，

∴，

∵，

∴，

∴当或时有一解，当时有两解；

（3）若P在DC上，设，，

∴，，

∴，

∵，

∴．

∴当时有一解，当时有两解；

（4）当点P在BC上时，设，，

∴，，

∴，

∵，

∴，

∴当或时有一解，当时有两解，

综上，在正方形的四条边上有且只有6个不同的点P，使得成立，那么m的取值范围是，

故答案为：．