题目内容
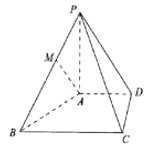
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.
(1)若![]() ,则在线段
,则在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由
点的位置;若不存在,请说明理由
(2)己知![]() ,若异面直线
,若异面直线![]() 与
与![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
【答案】(1)存在,点![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的一个三等分点;(2)2.
的一个三等分点;(2)2.
【解析】
(1) 延长![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() 。通过证明
。通过证明![]() 及
及![]() ,
,![]() 可得M为PB上的一个三等分点,且靠近点P。
可得M为PB上的一个三等分点,且靠近点P。
(2)建立空间直角坐标系,写出各个点的坐标,分别求得平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,再根据二面角夹角的余弦值即可得参数t的值,进而求得CD的长。
,再根据二面角夹角的余弦值即可得参数t的值,进而求得CD的长。
解:(1)延长![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 平面
平面![]() .
.
若![]() 平面
平面![]() ,由平面
,由平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() .
.
由![]() ,
,![]() ,则
,则![]() ,
,
故点![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的一个三等分点.
的一个三等分点.
(2)∵![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
则![]() 平面
平面![]()
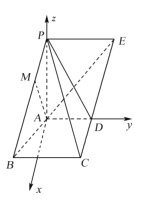
以点![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴,过点
轴,过点![]() 与平面
与平面![]() 垂直的直线为
垂直的直线为![]() 轴,建立如图所示的直角坐标系,
轴,建立如图所示的直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]()
设平面![]() 和平面
和平面![]() 的法向量分别为
的法向量分别为![]() ,
,![]() .
.
由![]() ,
,![]() 得
得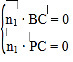 即
即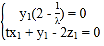 ,
,
令![]() ,则
,则![]() ,故
,故![]() .
.
同理可求得![]() .
.
于是 ,则
,则 ,解之得
,解之得![]() (负值舍去),故
(负值舍去),故![]() .
.
∴![]() .
.

【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
①先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用
的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,
元的人数,![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,随机变量
元的人数,随机变量![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
②小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?