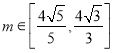题目内容
【题目】已知x,y,z均为正数.
(1)若xy<1,证明:|x+z||y+z|>4xyz;
(2)若![]() =
=![]() ,求2xy2yz2xz的最小值.
,求2xy2yz2xz的最小值.
【答案】(1)证明见解析;(2)最小值为8
【解析】
(1)利用基本不等式可得![]() , 再根据0<xy<1时, 即可证明|x+z||y+z|>4xyz.
, 再根据0<xy<1时, 即可证明|x+z||y+z|>4xyz.
(2)由![]() =
=![]() , 得
, 得![]() ,然后利用基本不等式即可得到xy+yz+xz≥3,从而求出2xy2yz2xz的最小值.
,然后利用基本不等式即可得到xy+yz+xz≥3,从而求出2xy2yz2xz的最小值.
(1)证明:∵x,y,z均为正数,
∴|x+z||y+z|=(x+z)(y+z)≥![]() =
=![]() ,
,
当且仅当x=y=z时取等号.
又∵0<xy<1,∴![]() ,
,
∴|x+z||y+z|>4xyz;
(2)∵![]() =
=![]() ,即
,即![]() .
.
∵![]() ,
,
![]() ,
,
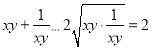 ,
,
当且仅当x=y=z=1时取等号,
∴![]() ,
,
∴xy+yz+xz≥3,∴2xy2yz2xz=2xy+yz+xz≥8,
∴2xy2yz2xz的最小值为8.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
【题目】近年来,人们支付方式发生巨大转变,使用移动支付购买商品已成为一部分人的消费习惯,某企业为了解该企业员工![]() 两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况,发现样本中
两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况,发现样本中![]() 两种支付方式都没有使用过的有5人;使用了
两种支付方式都没有使用过的有5人;使用了![]() 两种方式支付的员工,支付金额和相应人数分布如下表,依据数据估算:若从该公司随机抽取1名员工,则该员工在该月
两种方式支付的员工,支付金额和相应人数分布如下表,依据数据估算:若从该公司随机抽取1名员工,则该员工在该月![]() 两种支付方式都使用过的概率为_______________
两种支付方式都使用过的概率为_______________
支付金额(元) 支付方式 |
|
| 大于2000 |
使用 | 18人 | 29人 | 23人 |
使用 | 10人 | 24人 | 21人 |