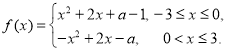题目内容
【题目】设直线
与抛物线
相交于
两点,与圆
：
相切于点
,且为线段
中点,若这样的直线恰有
条,则
的取值范围是
A. 
B. 
C. 
D. 
【答案】D
【解析】
假设A、B两点的坐标，圆心为C，求出点M的坐标，由垂直关系，利用斜率之积为-1列式，得到A、B横坐标的关系，由C、M两点间距离为半径也可列式，得到A、B横坐标间关系，由韦达定理逆推解为A、B横坐标的方程，有两个根，由判别式求出半径的范围，当斜率不存在时，也有两条直线，故共四条直线，即已求出半径范围.
设A、B两点的坐标分别为：
、
，则点M的坐标为：
，
圆心坐标为：C
，由于相切，所以
，
即：
，化简得：
，所以
，
由
可得：
，化简得：
，
所以
的两根分别为：
、
，
所以：
，解得：
，此时有两条直线，
当斜率为0时，已知存在两条直线满足题意，共四条.
故选D.
【题目】某书店刚刚上市了《中国古代数学史》，销售前该书店拟定了5种单价进行试销，每种单价（
元）试销l天，得到如表单价（元）与销量
（册）数据：
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
（l）根据表中数据，请建立关于的回归直线方程：
（2）预计今后的销售中，销量（册）与单价（元）服从（l）中的回归方程，已知每册书的成本是12元，书店为了获得最大利润，该册书的单价应定为多少元？
附：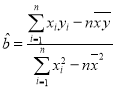
，
，
，
.
【题目】为积极响应国家“阳光体育运动”的号召，某学校在了解到学生的实际运动情况后，发起以“走出教室，走到操场，走到阳光”为口号的课外活动倡议。为调查该校学生每周平均体育运动时间的情况，从高一高二基础年级与高三三个年级学生中按照4:3:3的比例分层抽样，收集300位学生每周平均体育运动时间的样本数据(单位：小时)，得到如图所示的频率分布直方图。
（1）据图估计该校学生每周平均体育运动时间．并估计高一年级每周平均体育运动时间不足4小时的人数；
（2）规定每周平均体育运动时间不少于6小时记为“优秀”，否则为“非优秀”，在样本数据中，有30位高三学生的每周平均体育运动时间不少于6小时，请完成下列
列联表，并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”．
基础年级 | 高三 | 合计 | |
优秀 | |||
非优秀 | |||
合计 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附：K2
，n＝a+b+c+d．
