题目内容
【题目】已知函数f(x)=mln(x+1)﹣nx在点(1,f(1))处的切线与y轴垂直,且 ![]() ,其中 m,n∈R.
,其中 m,n∈R.
(Ⅰ)求m,n的值,并求出f(x)的单调区间;
(Ⅱ)设g(x)=﹣x2+2x,确定非负实数a的取值范围,使不等式f(x)+x≥ag(x)在[0,+∞)上恒成立.
【答案】解:(Ⅰ)对f(x)求导,得 ![]() ,
,
若f(x)在点(1,f(1))处的切线与y轴垂直,
则 ![]() ,又
,又 ![]() ,则
,则 ![]() ,
,
由 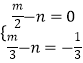 ,求得
,求得 ![]() ,
,
所以f(x)=2ln(x+1)﹣x,定义域为(﹣1,+∞),
对f(x)求导,得 ![]() ,
,
由f'(x)>0,求得﹣1<x<1,即f(x)的单调递增区间为(﹣1,1);
由f'(x)<0,求得x>1,即f(x)的单调递减区间为(1,+∞).
(Ⅱ)由(Ⅰ)知,不等式f(x)+x≥ag(x)即是2ln(x+1)≥a(﹣x2+2x),
于是问题可转化为不等式2ln(x+1)﹣a(﹣x2+2x)≥0在[0,+∞)上恒成立时,确定非负实数a的取值范围,
记h(x)=2ln(x+1)﹣a(﹣x2+2x),则 ![]() ,
,
① 当a=0时,对 ![]() ,则h(x)在[0,+∞)上为增函数,
,则h(x)在[0,+∞)上为增函数,
②当a>0时,令h'(x)=0,则ax2+1﹣a=0,当1﹣a≥0,
即0<a≤1时,对x≥0,h'(x)>0,则h(x)在[0,+∞)上为增函数,
所以h(x)=h(0)=0,此时命题成立;
当1﹣a<0,即a>1时,由ax2+1﹣a=0,
求得 ![]() .h(x),h'(x)的变化情况如表:
.h(x),h'(x)的变化情况如表:
x | 0 | (0,x2) | x2 | (x2 , +∞) |
h'(x) | ﹣ | 0 | + | |
h(x) | ↘ | 极小值 | ↗ |
因为h(x)min=h(x2)<h(0)=0,
所以当x≥0时,命题不成立
【解析】(Ⅰ)求出函数的导数,得到关于m,n的方程组,求出m,n的值,从而求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)问题可转化为不等式2ln(x+1)﹣a(﹣x2+2x)≥0在[0,+∞)上恒成立时,确定非负实数a的取值范围,记h(x)=2ln(x+1)﹣a(﹣x2+2x),根据函数的单调性求出a的范围即可.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案