��Ŀ����
����Ŀ�����г����飬ij��Ʒÿ�ֵļ۸�Ϊx��1��x��14����Ԫʱ������Ʒ���¹�����Ϊy1�֣�y1=ax+ ![]() a2��a��a��0������������Ϊy2�֣�y2=��
a2��a��a��0������������Ϊy2�֣�y2=�� ![]() x2��
x2�� ![]() x+1��������Ʒ�����������ڹ�����ʱ�����������ڹ�������������Ʒ�������������ڹ�����ʱ������������������������Ʒ�������۶��������������۸�ij˻���
x+1��������Ʒ�����������ڹ�����ʱ�����������ڹ�������������Ʒ�������������ڹ�����ʱ������������������������Ʒ�������۶��������������۸�ij˻���
��1����֪a= ![]() ����ij�¸���Ʒ�ļ۸�Ϊx=7������Ʒ�ڸ��µ����۶��ȷ��1Ԫ����
����ij�¸���Ʒ�ļ۸�Ϊx=7������Ʒ�ڸ��µ����۶��ȷ��1Ԫ����
��2�����������빩�������ʱ�ļ۸�Ϊ����۸�������Ʒ�ľ���۸���ÿ��6��Ԫ����ʵ��a��ȡֵ��Χ��
���𰸡�
��1���⣺��a= ![]() ��x=7ʱ��y1=
��x=7ʱ��y1= ![]() ��7+
��7+ ![]() ����
���� ![]() ��2��
��2�� ![]() =1+
=1+ ![]() ��
�� ![]() =
= ![]() ��
��
y2=�� ![]() ����
���� ![]() ��2��
��2�� ![]() ��
�� ![]() +1=
+1= ![]() ��
��
��y1��y2��
��������۶�Ϊ7�� ![]() ��104��50313��Ԫ��
��104��50313��Ԫ��
��2���⣺��f��x��=y1��y2= ![]() x2+��
x2+�� ![]() +a��x��a��1��
+a��x��a��1��
��f��x����[6��14��������㣬
��a��0����f��0��=��a��1��0����f��x����ͼ�����ϣ�
��f��x����[6��14����ֻ��1����㣬
�� ![]() ����
���� 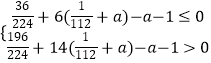 ��
��
��ã�0��a�� ![]()
����������1������y1 �� y2 �� �Ƚϴ�Сȷ�����������ټ������۶��2����f��x��=y1��y2 �� ��f��x����[6��14��������㣬�������Ĵ����Զ����в���ʽ����a�ķ�Χ��

 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�