题目内容
【题目】已知椭圆C1： 
+ 
=1（b＞0）的左、右焦点分别为F1、F2 ， 点F2也为抛物线C2：y2=8x的焦点，过点F2的直线l交抛物线C2于A，B两点．
（Ⅰ）若点P（8，0）满足|PA|=|PB|，求直线l的方程；
（Ⅱ）T为直线x=﹣3上任意一点，过点F1作TF1的垂线交椭圆C1于M，N两点，求 
的最小值．
【答案】解：（Ⅰ）由抛物线 
得F2（2，0），
当直线l斜率不存在，即l：x=2时，满足题意．
当直线l斜率存在，设l：y=k（x﹣2）（k≠0），A（x1，y1），B（x2，y2），
由 
得k2x2﹣（4k2+8）x+4k2=0，
∴ 
．
设AB的中点为G，则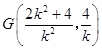 
，
∵|PA|=|PB|，∴PG⊥l，kPGk=﹣1，
∴ 
，解得 
，则 
，
∴直线l的方程为 或x=2．
（Ⅱ）∵F2（2，0），∴ 
，
设T点的坐标为（﹣3，m），
则直线TF1的斜率 
，
当m≠0时，直线MN的斜率 
，直线MN的方程是x=my﹣2，
当m=0时，直线MN的方程是x=﹣2，也符合x=my﹣2的形式．
∴直线MN的方程是x=my﹣2．
设M（x3，y3），N（x4，y4），则 
，得（m2+3）y2﹣4my﹣2=0，
∴ 
，
， 
= 
，
∴ 
，
当且仅当 
，即m=±1时，等号成立，此时 
取得最小值 
．
【解析】（Ⅰ）由抛物线 
得F2（2，0），当直线l斜率不存在，即l：x=2时，满足题意．当直线l斜率存在，设l：y=k（x﹣2）（k≠0），A（x1，y1），B（x2，y2），与抛物线方程联立可得k2x2﹣（4k2+8）x+4k2=0，利用根与系数的关系、中点坐标公式可得AB的中点 
，由|PA|=|PB|，可得PG⊥l，kPGk=﹣1，解得k即可得出．（Ⅱ）F2（2，0），可得椭圆C1的方程，设T点的坐标为（﹣3，m），则直线TF1的斜率 
=﹣m．当m≠0时，直线MN的斜率 
，直线MN的方程是x=my﹣2，
当m=0时，上述方程．设M（x3，y3），N（x4，y4），与椭圆的方程联立，利用根与系数的关系、两点之间的距离公式及其基本不等式的性质即可得出．
