╠Ō─┐─┌╚▌
ĪŠ╠Ō─┐Ī┐╔Ķa1 Ż¼ a2 Ż¼ ĪŁŻ¼an╬¬1Ż¼2Ż¼ĪŁŻ¼n░┤╚╬ęŌ╦│ą“ū÷│╔Ą─ę╗Ė÷┼┼┴ąŻ¼fk╩Ū╝»║Ž{ai|aiŻ╝ak Ż¼ iŻŠk}į¬╦žĄ─Ė÷╩²Ż¼Č°gk╩Ū╝»║Ž{ai|aiŻŠak Ż¼ iŻ╝k}į¬╦žĄ─Ė÷╩²Ż©k=1Ż¼2Ż¼ĪŁŻ¼nŻ®Ż¼╣µČ©fn=g1=0Ż¼└²╚ńŻ║Čįė┌┼┼┴ą3Ż¼1Ż¼2Ż¼f1=2Ż¼f2=0Ż¼f3=0
Ż©IŻ®Čįė┌┼┼┴ą4Ż¼2Ż¼5Ż¼1Ż¼3Ż¼Ū¾![]()
![]()
Ż©IIŻ®Čįė┌ŽŅ╩²╬¬2n®ü1 Ą─ę╗Ė÷┼┼┴ąŻ¼╚¶ę¬Ū¾2n®ü1╬¬Ė├┼┼┴ąĄ─ųą╝õŽŅŻ¼╩įŪ¾![]()
![]() Ą─ūŅ┤¾ųĄŻ¼▓óą┤│÷ŽÓė”Ą├ę╗Ė÷┼┼┴ą
Ą─ūŅ┤¾ųĄŻ¼▓óą┤│÷ŽÓė”Ą├ę╗Ė÷┼┼┴ą
Ż©ó¾Ż®ųż├„![]()
![]() =
=![]()
![]()
ĪŠ┤░ĖĪ┐ĮŌŻ║Ż©IŻ®Ī▀┼┼┴ą4Ż¼2Ż¼5Ż¼1Ż¼3Ż¼
fk╩Ū╝»║Ž{ai|aiŻ╝ak Ż¼ iŻŠk}į¬╦žĄ─Ė÷╩²Ż¼
ĪÓf1=3Ż¼f2=1Ż¼f3=2Ż¼f4=0Ż¼f5=0Ż¼
ĪÓ![]()
![]() =3+1+2+0+0=6Ż«
=3+1+2+0+0=6Ż«
Ż©IIŻ®Ą▒ŽŅ╩²╬¬2n®ü1 Ą─ę╗Ė÷┼┼┴ąŻ¼
2n®ü1╬¬Ė├┼┼┴ąĄ─ųą╝õŽŅŻ¼Ū░├µėąnŽŅŻ¼║¾├µėąnŽŅŻ¼
ĪÓę¬Ū¾![]()
![]() Ą─ūŅ┤¾ųĄŻ¼ų╗ę¬╩╣Ą├┼┼┴ą┬·ūŃnĄĮ2n®ü2┼┼┴ąĄĮ2n®ü1Ą─Ū░├µŻ¼1ĄĮn®ü1┼┼┴ąĄĮ2n®ü1Ą─║¾├µŻ¼
Ą─ūŅ┤¾ųĄŻ¼ų╗ę¬╩╣Ą├┼┼┴ą┬·ūŃnĄĮ2n®ü2┼┼┴ąĄĮ2n®ü1Ą─Ū░├µŻ¼1ĄĮn®ü1┼┼┴ąĄĮ2n®ü1Ą─║¾├µŻ¼
ĪÓg1=0Ż¼g2=1Ż¼g3=2Ż¼ĪŁg2n®ü1=2n®ü2Ż¼
ĪÓ![]()
![]() Ą─ūŅ┤¾ųĄ╩Ū
Ą─ūŅ┤¾ųĄ╩Ū![]() =Ż©2n®ü1Ż®Ż©n®ü1Ż®
=Ż©2n®ü1Ż®Ż©n®ü1Ż®
▒╚╚ńŠ┘ę╗Ė÷░³║¼7ŽŅĄ─╩²┴ąŻ║6Ż¼5Ż¼4Ż¼7Ż¼3Ż¼2Ż¼1
Ż©IIIŻ®Ī▀fk╩Ū╝»║Ž{ai|aiŻ╝ak Ż¼ iŻŠk}į¬╦žĄ─Ė÷╩²Ż¼
Č°gk╩Ū╝»║Ž{ai|aiŻŠak Ż¼ iŻ╝k}į¬╦žĄ─Ė÷╩²Ż©k=1Ż¼2Ż¼ĪŁŻ¼nŻ®Ż¼
╣µČ©fn=g1=0Ż¼
ĪÓfn®ü1=g2
fn®ü2=g3
ĪŁ
ĪÓf1=gn Ż«
ĪÓ![]()
![]() =
=![]()
![]()
ĪŠĮŌ╬÷Ī┐Ż©IŻ®ų▒Įė░┤Č©ęÕ└┤▓┘ū„Ż¼Ė∙Š▌fk╩Ū╝»║Ž{ai|aiŻ╝ak Ż¼ iŻŠk}į¬╦žĄ─Ė÷╩²Ż¼┐┤│÷Ę¹║Ž╠§╝■Ą─į¬╦žĄ─Ė÷╩²Ż¼Ą├ĄĮĮß╣¹Ż«
Ż©IIŻ®Ż©IIŻ®Ą▒ŽŅ╩²╬¬2n®ü1 Ą─ę╗Ė÷┼┼┴ąŻ¼2n®ü1╬¬Ė├┼┼┴ąĄ─ųą╝õŽŅŻ¼Ū░├µėąnŽŅŻ¼║¾├µėąnŽŅŻ¼ę¬Ū¾![]()
![]() Ą─ūŅ┤¾ųĄŻ¼ų╗ę¬╩╣Ą├┼┼┴ą┬·ūŃnĄĮ2n®ü2┼┼┴ąĄĮ2n®ü1Ą─Ū░├µŻ¼1ĄĮn®ü1┼┼┴ąĄĮ2n®ü1Ą─║¾├µŻ¼Ą├ĄĮĮß╣¹Ż«
Ą─ūŅ┤¾ųĄŻ¼ų╗ę¬╩╣Ą├┼┼┴ą┬·ūŃnĄĮ2n®ü2┼┼┴ąĄĮ2n®ü1Ą─Ū░├µŻ¼1ĄĮn®ü1┼┼┴ąĄĮ2n®ü1Ą─║¾├µŻ¼Ą├ĄĮĮß╣¹Ż«
Ż©IIIŻ®fk╩Ū╝»║Ž{ai|aiŻ╝ak Ż¼ iŻŠk}į¬╦žĄ─Ė÷╩²Ż¼Č°gk╩Ū╝»║Ž{ai|aiŻŠak Ż¼ iŻ╝k}į¬╦žĄ─Ė÷╩²Ż©k=1Ż¼2Ż¼ĪŁŻ¼nŻ®Ż¼╣µČ©fn=g1=0Ż¼ę└┤╬Ą├ĄĮfn®ü1=g2 Ż¼ ĪŁŻ¼Ą├ĄĮĖ„ŽŅų«║═ŽÓĄ╚Ż«
ĪŠ┐╝ĄŃŠ½╬÷Ī┐▒Š╠Ōų„ę¬┐╝▓ķ┴╦╩²┴ąĄ─Ū░nŽŅ║═Ą─ŽÓ╣žų¬╩ČĄŃŻ¼ąĶ꬚Ų╬š╩²┴ą{an}Ą─Ū░nŽŅ║═snėļ═©ŽŅanĄ─╣žŽĄ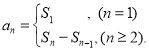 ▓┼─▄š²╚ĘĮŌ┤┤╦╠ŌŻ«
▓┼─▄š²╚ĘĮŌ┤┤╦╠ŌŻ«

ĪŠ╠Ō─┐Ī┐─│蹊┐╗·╣╣╬¬┴╦Ą„蹥▒┤·ųą╣·Ė▀ųą╔·Ą─ŲĮŠ∙─Ļ┴õŻ¼┤ėĖ„ĄžČÓ╦∙Ė▀ųą╦µ╗·│ķ╚Ī┴╦40├¹č¦╔·Į°ąą─Ļ┴õ═│╝ŲŻ¼Ą├ĄĮĮß╣¹╚ńŽ┬▒Ē╦∙╩ŠŻ║
─Ļ┴õŻ©╦ĻŻ® |
|
|
|
|
|
╩²┴┐ | 6 | 10 | 12 | 8 | 4 |
(ó±)╚¶═¼ę╗ūķ╩²Š▌ė├Ė├ūķŪ°╝õĄ─ųąĄŃųĄ┤·▒ĒŻ¼╩į╣└╝ŲšŌ┼·č¦╔·Ą─ŲĮŠ∙─Ļ┴õŻ╗
(ó“)╚¶į┌▒Š┤╬│ķ│÷Ą─č¦╔·ųą╦µ╗·╠¶čĪ2╚╦Ż¼╝Ū─Ļ┴õį┌![]() ╝õĄ─č¦╔·╚╦╩²╬¬
╝õĄ─č¦╔·╚╦╩²╬¬![]() Ż¼Ū¾
Ż¼Ū¾![]() Ą─Ęų▓╝┴ą╝░╩²č¦Ų┌═¹.
Ą─Ęų▓╝┴ą╝░╩²č¦Ų┌═¹.


