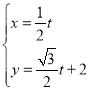Question

【题目】某学校为调查高三年级学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图(如图(1))和女生身高情况的频率分布直方图(如图(2))．已知图(1)中身高在170～175cm的男生有16名．

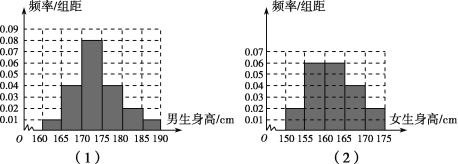
（1）试问在抽取的学生中，男、女生各有多少名？

	身高≥170cm	身高<170cm	总计
男生
女生
总计

（2）根据频率分布直方图，完成下面的2×2列联表，并判断能有多大(百分数)的把握认为身高与性别有关？

附：参考公式和临界值表

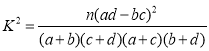
	0.050	0.010	0.001
	3.841	6.635	10.828

Answer 1

【答案】（1）男生40名，女生40名（2）见解析，能有99.9%的把握认为身高与性别有关．

【解析】

（1）由图（1）求出男生的人数为40，所以女生人数为40；

（2）完成列联表后，根据公式计算出，结合临界值表可得结论.

解：(1)由题图(1)可知，身高在170～175 cm的男生的频率为0.08×5＝0.4，设抽取的学生中，男生有n1名，则，解得n1＝40.

所以女生有80－40＝40(名)．

(2)由(1)及频率分布直方图知，身高≥170 cm的男生有(0.08＋0.04＋0.02＋0.01)×5×40＝30(名)，身高≥170 cm的女生有0.02×5×40＝4(名)，所以可得下列列联表：

	身高≥170cm	身高<170cm	总计
男生	30	10	40
女生	4	36	40
总计	34	46	80

由列联表中数据得K2的观测值为≈34.578>10.828.

所以能有99.9%的把握认为身高与性别有关．