题目内容
【题目】平面直角坐标系中，以原点
为圆心，
为半径的定圆
，与过原点且斜率为
的动直线交于
、
两点，在
轴正半轴上有一个定点
，、、
三点构成三角形，求：
（1）△
的面积
的表达式，并求出的取值范围；
（2）△的外接圆
的面积
的表达式，并求出的取值范围.
【答案】（1）
,
；（2）
， 
.
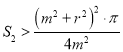【解析】
（1）求得
到直线
的距离，由此求得三角形
的面积
的表达式，并由此求得的取值范围.
（2）设动直线的倾斜角为
，根据题意得到
.设出
的坐标，利用三角形外接圆半径公式求得三角形外接圆半径的表达式，由此求得
，并求得的取值范围.
（1）
到直线
的距离为
，所以三角形的面积为
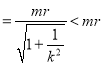.所以.
（2）设动直线的倾斜角为，
，则.画出图像如下图所示.设
，而.所以
，
，
.由（1）得
. 所以三角形的外接圆半径为
.所以.由于
，所以
，即.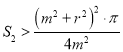
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】某餐厅通过查阅了最近5次食品交易会参会人数
(万人)与餐厅所用原材料数量
(袋)，得到如下统计表：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
（1）根据所给5组数据，求出
关于
的线性回归方程
.
（2）已知购买原材料的费用
(元)与数量
(袋)的关系为
，
投入使用的每袋原材料相应的销售收入为700元，多余的原材料只能无偿返还，据悉本次交易大会大约有15万人参加，根据(1)中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？(注：利润
销售收入
原材料费用).
参考公式： 
， 
.
参考数据： 
， 
， 
.
【题目】某学校为调查高三年级学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图(如图(1))和女生身高情况的频率分布直方图(如图(2))．已知图(1)中身高在170～175cm的男生有16名．
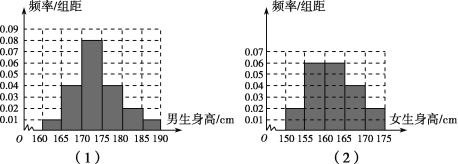
（1）试问在抽取的学生中，男、女生各有多少名？
身高≥170cm | 身高<170cm | 总计 | |
男生 | |||
女生 | |||
总计 |
（2）根据频率分布直方图，完成下面的2×2列联表，并判断能有多大(百分数)的把握认为身高与性别有关？
附：参考公式和临界值表
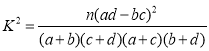
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
