题目内容
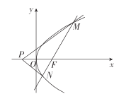
【题目】如图,已知点F为抛物线C:![]() (
(![]() )的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为45°时,
)的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为45°时,![]() .
.
(1)求抛物线C的方程.
(2)试确定在x轴上是否存在点P,使得直线PM,PN关于x轴对称?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)存在唯一的点
(2)存在唯一的点![]() ,使直线PM,PN关于x轴对称
,使直线PM,PN关于x轴对称
【解析】
(1)当直线l的倾斜角为45°,则![]() 的斜率为1,则直线方程为
的斜率为1,则直线方程为![]() ,联立直线与抛物线方程,利用韦达定理可得
,联立直线与抛物线方程,利用韦达定理可得![]() ,根据焦点弦公式
,根据焦点弦公式![]() ,求出
,求出![]() 的值,即可得到抛物线方程.
的值,即可得到抛物线方程.
(2)假设满足条件的点P存在,设![]() ,当直线l不与x轴垂直时,设l的方程为
,当直线l不与x轴垂直时,设l的方程为![]() (
(![]() ),联立直线与抛物线方程,消元,列出韦达定理,因为直线PM,PN关于x轴对称,所以
),联立直线与抛物线方程,消元,列出韦达定理,因为直线PM,PN关于x轴对称,所以![]() ,即可求出
,即可求出![]() 的值. 当直线l与x轴垂直时,由抛物线的对称性,易知PM,PN关于x轴对称,此时只需P与焦点F不重合即可.
的值. 当直线l与x轴垂直时,由抛物线的对称性,易知PM,PN关于x轴对称,此时只需P与焦点F不重合即可.
解:(1)当直线l的倾斜角为45°,则![]() 的斜率为1,
的斜率为1,
![]() ,
,![]() 的方程为
的方程为![]() .
.
由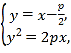 得
得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
∴抛物线C的方程为![]() .
.
(2)假设满足条件的点P存在,设![]() ,由(1)知
,由(1)知![]() ,
,
①当直线l不与x轴垂直时,设l的方程为![]() (
(![]() ),
),
由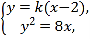 得
得![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
∵直线PM,PN关于x轴对称,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∴![]() 时,此时
时,此时![]() .
.
②当直线l与x轴垂直时,由抛物线的对称性,
易知PM,PN关于x轴对称,此时只需P与焦点F不重合即可.
综上,存在唯一的点![]() ,使直线PM,PN关于x轴对称.
,使直线PM,PN关于x轴对称.

 阅读快车系列答案
阅读快车系列答案【题目】为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算K2=8.01,附表如下:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参照附表,得到的正确的结论是( )
A. 有99%以上的把握认为“喜欢乡村音乐与性别有关”
B. 有99%以上的把握认为“喜欢乡村音乐与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别无关”
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【题目】在信息时代的今天,随着手机的发展,“微信”越来越成为人们交流的一种方法,某机构对“使用微信交流”的态度进行调查,随机抽取了100人,他们年龄的频数分布及对“使用微信交流”赞成的人数如下表:(注:年龄单位:岁)
年龄 |
|
|
|
|
|
|
频数 | 10 | 30 | 30 | 20 | 5 | 5 |
赞成人数 | 9 | 25 | 24 | 9 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的![]() 列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() ,
,![]() 调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.