题目内容
设{an}是公比为正数的等比数列,a1=2,a3=a2+4.
(1)求{an}的通项公式.
(2)设{bn}是首项为1,公差为2的等差数列,求{an+bn}的前n项和Sn.
(1)求{an}的通项公式.
(2)设{bn}是首项为1,公差为2的等差数列,求{an+bn}的前n项和Sn.
(1)an==2n (2)Sn=2n+1+n2-2
(1)设{an}的公比为q,且q>0,
由a1=2,a3=a2+4,
所以2q2=2q+4,即q2-q-2=0,
又q>0,解之得q=2.
所以{an}的通项公式an=2·2n-1=2n.
(2)Sn=(a1+b1)+(a2+b2)+…+(an+bn)=(a1+a2+…+an)+(b1+b2+…+bn)
= +n×1+
+n×1+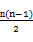 ×2
×2
=2n+1+n2-2.
由a1=2,a3=a2+4,
所以2q2=2q+4,即q2-q-2=0,
又q>0,解之得q=2.
所以{an}的通项公式an=2·2n-1=2n.
(2)Sn=(a1+b1)+(a2+b2)+…+(an+bn)=(a1+a2+…+an)+(b1+b2+…+bn)
=
 +n×1+
+n×1+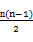 ×2
×2=2n+1+n2-2.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 的前
的前 项和记为
项和记为 ,
, ,
,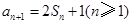 .
. 的各项为正,其前
的各项为正,其前 ,且
,且 ,又
,又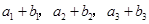 成等比数列,求
成等比数列,求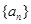 满足
满足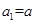 且
且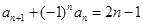 (其中
(其中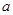 为常数),
为常数),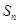 是数列
是数列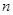 项和,数列
项和,数列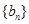 满足
满足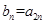 .
.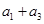 的值;
的值; 猜想
猜想 的表达式为( )
的表达式为( )







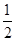 ,
,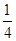 ,…,
,…,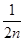 ,….是( )
,….是( )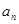 }的前
}的前 项和
项和 ,则
,则 的值为 ( )
的值为 ( ) 


