题目内容
数列 的前
的前 项和记为
项和记为 ,
, ,
,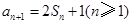 .
.
(1)求证 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(2)等差数列 的各项为正,其前
的各项为正,其前 项和为
项和为 ,且
,且 ,又
,又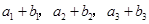 成等比数列,求
成等比数列,求 .
.
 的前
的前 项和记为
项和记为 ,
, ,
,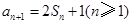 .
.(1)求证
 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;(2)等差数列
 的各项为正,其前
的各项为正,其前 项和为
项和为 ,且
,且 ,又
,又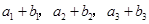 成等比数列,求
成等比数列,求 .
.(1)证明见解析, ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)对于
 可得
可得 两式相减化得
两式相减化得 ,又
,又 ,所以
,所以 为等比数列,首项为1,公比为3,可写出通项公式;(2)令等差数列
为等比数列,首项为1,公比为3,可写出通项公式;(2)令等差数列 公差为d,由
公差为d,由 ,得
,得 ,又
,又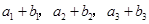 成等比数列,可得
成等比数列,可得 ,解得d,可得等差数列的前n 项和.
,解得d,可得等差数列的前n 项和.解:(1)由
 可得
可得 ,
,两式相减得
 ,
, .
.又
 ,
, .……4分
.……4分故
 是首项为1,公比为3的等比数列,
是首项为1,公比为3的等比数列, .
.(2)设
 的公差为
的公差为 ,由
,由 得
得 ,可得
,可得 ,
,故可设
 ,
,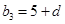 ,又
,又 ,
, ,
,由题意可得
 ,
,解得
 ,
, .
. 等差数列
等差数列 的各项为正,
的各项为正, .
. ,
, .
.
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 和
和 ,前
,前 项和分别为
项和分别为 ,且
,且 则
则 等于 。
等于 。 的前100项和为( )
的前100项和为( )



 升
升 升
升 升
升 的前
的前 项和为
项和为 ,向量
,向量 ,(
,(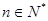 )满足
)满足 .
. 的通项公式为
的通项公式为 (
( ),若
),若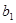 ,
, ,
, (
( )成等差数列,求
)成等差数列,求 和
和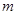 的值;
的值; 满足
满足 ,公比
,公比 满足
满足 ,且对任意正整数
,且对任意正整数 ,
, 仍是该数列中的某一项,求公比
仍是该数列中的某一项,求公比 ,若
,若 ,记
,记 为
为 项和,则使
项和,则使 达到最大的
达到最大的 中,
中, ,前
,前 项和
项和 ,则
,则 等于( )
等于( )


