题目内容
若数列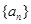 满足
满足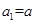 且
且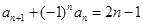 (其中
(其中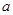 为常数),
为常数),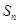 是数列
是数列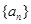 的前
的前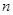 项和,数列
项和,数列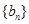 满足
满足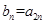 .
.
(1)求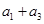 的值;
的值;
(2)试判断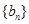 是否为等差数列,并说明理由;
是否为等差数列,并说明理由;
(3)求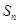 (用
(用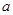 表示).
表示).
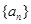 满足
满足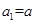 且
且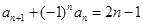 (其中
(其中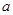 为常数),
为常数),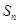 是数列
是数列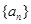 的前
的前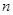 项和,数列
项和,数列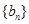 满足
满足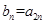 .
.(1)求
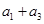 的值;
的值;(2)试判断
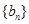 是否为等差数列,并说明理由;
是否为等差数列,并说明理由;(3)求
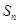 (用
(用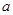 表示).
表示). (1) ;(2)当
;(2)当 时,数列
时,数列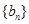 为等差数列;当
为等差数列;当 时,数列
时,数列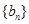 不为等差数列;(3)
不为等差数列;(3)

 ;(2)当
;(2)当 时,数列
时,数列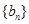 为等差数列;当
为等差数列;当 时,数列
时,数列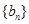 不为等差数列;(3)
不为等差数列;(3)
试题分析:(1)根据题意取
 时,即得
时,即得 ,可求出
,可求出  ;(2)由题中所给条件:
;(2)由题中所给条件: 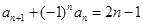 ,结合题中目标不难得到:
,结合题中目标不难得到: ,两式相加后得:
,两式相加后得:  ,即
,即 ,再替换一下即可得:
,再替换一下即可得: ,联想与等差数列列的定义可得:
,联想与等差数列列的定义可得: ,再单独考虑一下前三项即:当且仅当
,再单独考虑一下前三项即:当且仅当 ,
, ,
,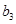 为等差数列,数列
为等差数列,数列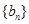 为等差数列,可求得
为等差数列,可求得 ,即可得出结论;(3)由题中所给条件
,即可得出结论;(3)由题中所给条件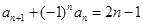 ,可替换得
,可替换得 ,进一步可化简得:
,进一步可化简得:  ,即
,即 ,这样就可求出:
,这样就可求出:  ,即可得:
,即可得:  ;而再由(2)中所求
;而再由(2)中所求 ,又因为
,又因为 ,则可得
,则可得 ,
,  ,由
,由 ,这样就可求出另外三种情形:
,这样就可求出另外三种情形:  ,
, ,
, ,即问题可求解.
,即问题可求解.(1)由题意,得
 ,
,
 . 4分
. 4分(2)

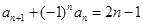 ,
,
 ,
,
 ,即
,即 ,
,
 ,
,
 ,于是当且仅当
,于是当且仅当 ,
, ,
,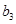 为等差数列,数列
为等差数列,数列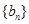 为等差数列, 7分
为等差数列, 7分又
 ,
,
 ,
, 
 ,
,
 ,
,
 ,
,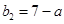 ,
, ,由
,由 ,
, ,
,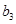 为等差数列,得
为等差数列,得 ,
, 当
当 时,数列
时,数列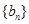 为等差数列;当
为等差数列;当 时,数列
时,数列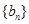 不为等差数列. 10分
不为等差数列. 10分(3)

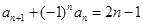 ,
,
 ,
,
 ,即
,即 ,
,
 ,
,


 ,
,
 ,
,
 . 13分
. 13分由(2)
 ,
,
 ,
,
 ,
,  ,
,由
 ,
,
 ,
,
 ,
,又
 ,
,
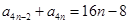 ,
, ,
,
 ,
, ,
, ,
,
 16分
16分
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 同时满足:(1)各项均为正数,(2)存在常数k, 对任意
同时满足:(1)各项均为正数,(2)存在常数k, 对任意 都成立,那么,这样的数列
都成立,那么,这样的数列 , a2、a4、a5成等差数列,求的值;
, a2、a4、a5成等差数列,求的值; 对任意
对任意 都成立?若存在,求出λ;若不存在,说明理由.
都成立?若存在,求出λ;若不存在,说明理由. 和
和 ,前
,前 项和分别为
项和分别为 ,且
,且 则
则 等于 。
等于 。 的前
的前 项和为
项和为 ,向量
,向量 ,(
,(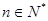 )满足
)满足 .
. 的通项公式为
的通项公式为 (
( ),若
),若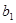 ,
, ,
, (
( )成等差数列,求
)成等差数列,求 和
和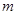 的值;
的值; 满足
满足 ,公比
,公比 满足
满足 ,且对任意正整数
,且对任意正整数 ,
, 仍是该数列中的某一项,求公比
仍是该数列中的某一项,求公比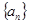 的前
的前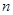 项和为
项和为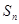 ,
,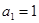 ,且
,且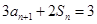 (
(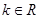 ,使得
,使得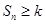 恒成立?若存在,求是实数
恒成立?若存在,求是实数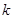 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.  中,
中, ,前
,前 项和
项和 ,则
,则 等于( )
等于( )



 为等差数列
为等差数列 的前
的前 项和,
项和, ,则
,则 =
=

