题目内容
13．已知偶函数f（x）是[0，+∞）上单调递减，满足不等式f（2a-1）＜f（1），则实数a的取值范围是（-∞，0）∪（1，+∞）．分析 根据函数奇偶性和单调性之间的关系进行转化即可．
解答 解：∵偶函数f（x）是[0，+∞）上单调递减，满足不等式f（2a-1）＜f（1），
∴不等式等价为f（|2a-1|）＜f（1），
即|2a-1|＞1，
即2a-1＞1或2a-1＜-1，
即a＞1或a＜0，
故答案为：（-∞，0）∪（1，+∞）
点评 本题主要考查不等式的求解，根据函数奇偶性和单调性之间的关系，将不等式进行转化是解决本题的关键．
练习册系列答案
相关题目
1．
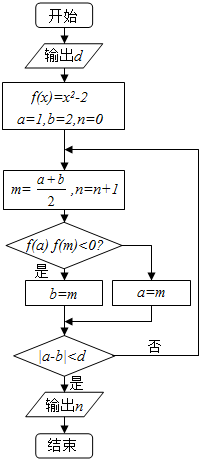执行如图的程序框图，如果输入的d=0.01，则输出的n=（ ）
执行如图的程序框图，如果输入的d=0.01，则输出的n=（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
8．设函数f（x）是定义在R上的偶函数，对任意x∈R，都有f（x+2）=f（x-2），且当x∈[-2，0]时，f（x）=（$\frac{1}{2}$）x-1，若在区间（-2，6]内关于x的方程f（x）-loga（x+2）=0（a＞1）至少有2个不同的实数根，至多有3个不同的实数根，则a的取值范围是（ ）
| A． | （1，2） | B． | （2，+∞） | C． | $（{1，\root{3}{4}}）$ | D． | $[{\root{3}{4}，2}）$ |
5．已知函数f（x）=x3-2x2+2，则下列区间必存在零点的是（ ）
| A． | （$-2，-\frac{3}{2}$） | B． | （$-\frac{3}{2}，-1）$ | C． | （$-1，-\frac{1}{2}$） | D． | （$-\frac{1}{2}，0$） |
2．已知实数x，y满足条件$\left\{\begin{array}{l}{x+y≤4}\\{y≥x}\\{x≥1}\end{array}\right.$，设Z=$\frac{y}{x+1}$，则Z的取值范围（ ）
| A． | （-∞，$\frac{1}{2}$] | B． | [$\frac{1}{2}$，$\frac{3}{2}$] | C． | [$\frac{3}{2}$，+∞） | D． | （-∞，$\frac{1}{2}$]∪[$\frac{3}{2}$，+∞） |