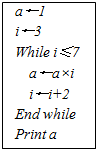Question

2．已知实数x，y满足条件$\left\{\begin{array}{l}{x+y≤4}\\{y≥x}\\{x≥1}\end{array}\right.$，设Z=$\frac{y}{x+1}$，则Z的取值范围（　　）

• A． （-∞，$\frac{1}{2}$]
• B． [$\frac{1}{2}$，$\frac{3}{2}$]
• C． [$\frac{3}{2}$，+∞）
• D． （-∞，$\frac{1}{2}$]∪[$\frac{3}{2}$，+∞）

Answer 1

分析 作出可行域，Z=$\frac{y}{x+1}$表示区域内的点与（-1，0）连线的斜率，数形结合可得．

解答 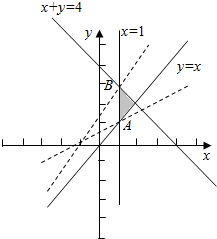解：作出$\left\{\begin{array}{l}{x+y≤4}\\{y≥x}\\{x≥1}\end{array}\right.$所对应的区域（如图阴影），
目标函数Z=$\frac{y}{x+1}$表示区域内的点与（-1，0）连线的斜率，
当直线经过点A（1，1）时，z取最小值$\frac{1}{2}$，
当直线经过点B（1，3）时，z取最大值$\frac{3}{2}$，
故选：B

点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．