题目内容
8.设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+2)=f(x-2),且当x∈[-2,0]时,f(x)=($\frac{1}{2}$)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)至少有2个不同的实数根,至多有3个不同的实数根,则a的取值范围是( )| A. | (1,2) | B. | (2,+∞) | C. | $({1,\root{3}{4}})$ | D. | $[{\root{3}{4},2})$ |
分析 由题意可知f(x)是定义在R上的周期为4的函数;从而作函数f(x)与y=loga(x+2)的图象,从而结合图象解得.
解答 解:∵对x∈R,都有f(x-2)=f(x+2),
∴f(x)是定义在R上的周期为4的函数;
作函数f(x)与y=loga(x+2)的图象如下,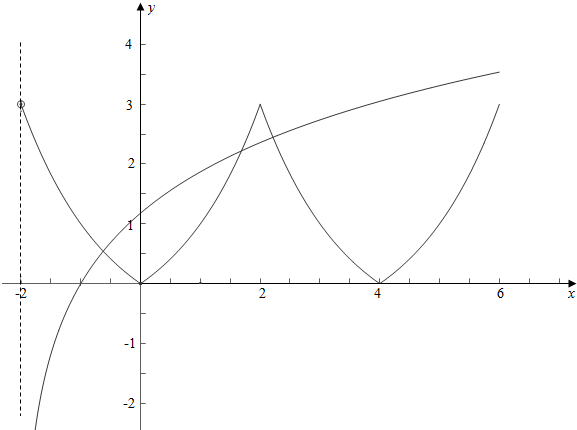 ,
,
结合图象可知,$\left\{\begin{array}{l}{lo{g}_{a}(2+2)≤3}\\{lo{g}_{a}(2+6)>3}\end{array}\right.$,
解得,$\root{3}{4}$≤a<2;
故选D.
点评 本题考查了数形结合的思想应用及方程的根与函数的图象的交点的关系应用.

练习册系列答案
相关题目
19.函数$f(x)=\left\{\begin{array}{l}(1-3a)x+2,x≤1\\{a^x},x>1\end{array}\right.$是R上的减函数,则实数a的取值范围为( )
| A. | $(\frac{1}{3},1)$ | B. | $[\frac{3}{4},1)$ | C. | $(\frac{1}{3},\frac{3}{4})$ | D. | $(\frac{1}{3},\frac{3}{4}]$ |
