题目内容
1.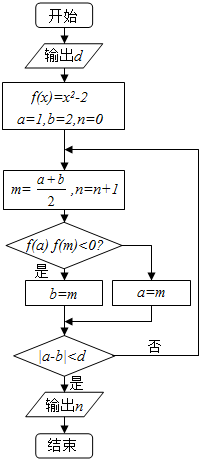 执行如图的程序框图,如果输入的d=0.01,则输出的n=( )
执行如图的程序框图,如果输入的d=0.01,则输出的n=( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 模拟执行程序框图,依次写出每次循环得到的m,n,a,b的值,当b=$\frac{3}{2}$,a=$\frac{191}{128}$时满足条件:|a-b|<0.001,退出循环,输出n的值为7.
解答 解:模拟执行程序框图,可得
a=1,b=2,n=0,
m=$\frac{3}{2}$,n=1
满足条件:f(1)•f($\frac{3}{2}$)<0,b=$\frac{3}{2}$,
不满足条件:|a-b|<0.001,m=$\frac{5}{4}$,n=2,不满足条件:f(1)•f($\frac{5}{4}$)<0,a=$\frac{5}{4}$,
不满足条件:|a-b|<0.001,m=$\frac{11}{8}$,n=3,不满足条件:f($\frac{5}{4}$)•f($\frac{11}{8}$)<0,a=$\frac{11}{8}$,
不满足条件:|a-b|<0.001,m=$\frac{23}{16}$,n=4,不满足条件:f($\frac{11}{8}$)•f($\frac{23}{16}$)<0,a=$\frac{23}{16}$,
不满足条件:|a-b|<0.001,m=$\frac{47}{32}$,n=5,不满足条件:f($\frac{23}{16}$)•f($\frac{47}{32}$)<0,a=$\frac{47}{32}$,
不满足条件:|a-b|<0.001,m=$\frac{95}{64}$,n=6,不满足条件:f($\frac{47}{32}$)•f($\frac{95}{64}$)<0,a=$\frac{95}{64}$,
不满足条件:|a-b|<0.001,m=$\frac{191}{128}$,n=7,不满足条件:f($\frac{95}{64}$)•f($\frac{191}{128}$)<0,a=$\frac{191}{128}$,
满足条件:|a-b|<0.001,退出循环,输出n的值为7.
故选:C.
点评 本题考查了直到型循环结构的程序框图,根据框图的流程判断算法的功能是解题的关键,属于基础题.

 高中必刷题系列答案
高中必刷题系列答案| A. | (1,2) | B. | $(0,\frac{1}{9})∪(9,+∞)$ | C. | $(0,\frac{1}{9})∪(1,9)$ | D. | $(\frac{1}{9},9)$ |
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
| A. | y=$\frac{1}{x}$ | B. | y=($\frac{1}{3}$)x | C. | y=x${\;}^{\frac{1}{2}}$ | D. | y=x2-2x-15 |