题目内容
【题目】如图,已知椭圆O: ![]() 的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
(1)当直线PM过椭圆的右焦点F时,求△FBM的面积;
(2)记直线BM,BP的斜率分别为k1,k2,求证:k1·k2为定值.
【答案】(1)![]() ,(2)见解析.
,(2)见解析.
【解析】试题分析:
(1)由题知B(0,1),C(0,-1), ![]() ,满足题意时,直线PM的方程为
,满足题意时,直线PM的方程为![]() ,与椭圆方程联立可得:
,与椭圆方程联立可得: 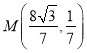 ,直线BF的方程为
,直线BF的方程为![]() ,则三角形的高为
,则三角形的高为![]() ,底边
,底边![]() ,三角形的面积为
,三角形的面积为![]() .
.
(2)设P(m,-2),且m≠0,则直线PM的方程为![]() ,与椭圆方程联立可得
,与椭圆方程联立可得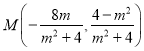 ,则
,则![]() ,据此可得k1·k2为定值
,据此可得k1·k2为定值![]() .
.
试题解析:
(1)由题知B(0,1),C(0,-1),焦点F(![]() ,0),
,0),
当直线PM过椭圆的右焦点F时,
直线PM的方程为![]() +
+![]() =1,即y=
=1,即y=![]() x-1.
x-1.
联立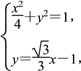 解得
解得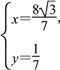 或
或![]() (舍),所以M
(舍),所以M![]() .连接BF,则直线BF的方程为
.连接BF,则直线BF的方程为![]() +
+![]() =1,
=1,
即x+![]() y-
y-![]() =0,
=0,
而BF=a=2,所以点M到直线BF的距离为
d=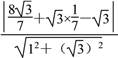 =
=![]() =
=![]() .
.
故S△MBF=![]() ·BF·d=
·BF·d=![]() ×2×
×2×![]() =
=![]() .
.
(2)设P(m,-2),且m≠0,
则直线PM的斜率为k=![]() =-
=-![]() ,
,
则直线PM的方程为y=-![]() x-1,
x-1,
联立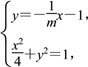 化简得
化简得![]() x2+
x2+![]() x=0,
x=0,
解得M![]() ,
,
所以k1=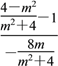 =
=![]() =
=![]() m,k2=
m,k2=![]() =-
=-![]() ,
,
所以k1·k2=-![]() ·
·![]() m=-
m=-![]() 为定值.
为定值.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?