题目内容
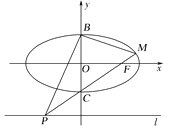
【题目】设椭圆
，B为椭圆上任一点，F为椭圆左焦点，已知
的最小值与最大值之和为4，且离心率
，抛物线
的通径为4．
求椭圆和抛物线的方程；
设坐标原点为O，A为直线
与已知抛物线在第一象限内的交点，且有
．
试用k表示A，B两点坐标；
是否存在过A，B两点的直线l，使得线段AB的中点在y轴上？若存在，求出直线l的方程，若不存在，请说明理由．
【答案】（1）椭圆方程为
，抛物线方程为
；（2）①
，
，
；②不存在.
【解析】
根据|
的最小值与最大值之和为4，可求出a=2，再根据离心率求出c，再求得
，则椭圆方程可得，根据抛物线
的通径为4，可得
，即可求出抛物线方程，
设直线OA方程为
，与抛物线方程联立，解得即可求出点A的坐标，根据设直线OB方程为
，将直线OB与椭圆联立，解得即可求出点B的坐标，
根据
的结论，利用线段AB的中点在y轴上，若求出k的值，在存在，否则不存在
解：
为椭圆上任一点，F为椭圆左焦点，
的最小值与最大值之和为4，
，
，
，
，
椭圆方程为，
抛物线的通径为4，
，
抛物线的方程为．
设直线OA方程为，显然
，将直线OA与抛物线联立：
得
，
，
，，
，
设直线OB方程为，将直线OB与椭圆联立：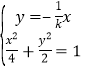
得
，
当
时，
，
，
，，
当
时，
，
，
，，
综上
，
，
，
当时，，
的中点在y轴上
，即
，此时方程无解，
当时，
，
，即
，此时方程无解，
综上可知，不存在这样的直线l，使得AB的中点在y轴上．
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y（万元）的几组对照数据:
x（年） | 2 | 3 | 4 | 5 | 6 |
y（万元） | 1 | 2.5 | 3 | 4 | 4.5 |
（1）若知道y对x呈线性相关关系，请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
；
（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低?参考公式: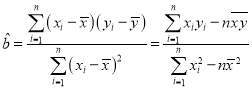
，
.
