题目内容
已知函数f(x)=2cosxsin(x+ )-
)-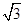 sin2x+sinxcosx.
sin2x+sinxcosx.
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象沿x轴向右平移m个单位后的图象关于直线x=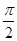 对称,求m的最小正值.
对称,求m的最小正值.
 )-
)-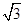 sin2x+sinxcosx.
sin2x+sinxcosx.(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象沿x轴向右平移m个单位后的图象关于直线x=
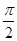 对称,求m的最小正值.
对称,求m的最小正值.(1)[kπ+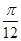 ,kπ+
,kπ+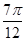 ],k∈Z
],k∈Z
(2)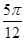
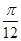 ,kπ+
,kπ+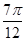 ],k∈Z
],k∈Z(2)
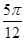
解:(1)f(x)=2cosx(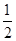 sinx+
sinx+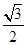 cosx)-
cosx)-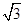 sin2x+sinxcosx
sin2x+sinxcosx
=sinxcosx+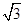 cos2x-
cos2x-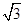 sin2x+sinxcosx
sin2x+sinxcosx
=sin2x+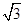 cos2x
cos2x
=2sin(2x+ ),
),
由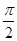 +2kπ≤2x+
+2kπ≤2x+ ≤2kπ+
≤2kπ+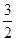 π,k∈Z,
π,k∈Z,
得kπ+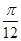 ≤x≤kπ+
≤x≤kπ+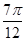 ,k∈Z.
,k∈Z.
故函数f(x)的单调递减区间为[kπ+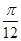 ,kπ+
,kπ+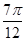 ],k∈Z.
],k∈Z.
(2)y=2sin(2x+ )―→y=2sin(2x+
)―→y=2sin(2x+ -2m),
-2m),
∵y=2sin(2x+ -2m)的图象关于直线x=
-2m)的图象关于直线x=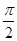 对称,
对称,
∴2·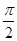 +
+ -2m=kπ+
-2m=kπ+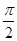 (k∈Z),
(k∈Z),
∴m=-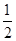 kπ+
kπ+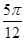 (k∈Z),
(k∈Z),
当k=0时,m的最小正值为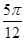 .
.
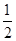 sinx+
sinx+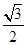 cosx)-
cosx)-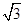 sin2x+sinxcosx
sin2x+sinxcosx=sinxcosx+
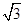 cos2x-
cos2x-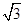 sin2x+sinxcosx
sin2x+sinxcosx=sin2x+
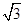 cos2x
cos2x=2sin(2x+
 ),
),由
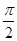 +2kπ≤2x+
+2kπ≤2x+ ≤2kπ+
≤2kπ+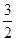 π,k∈Z,
π,k∈Z,得kπ+
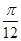 ≤x≤kπ+
≤x≤kπ+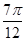 ,k∈Z.
,k∈Z.故函数f(x)的单调递减区间为[kπ+
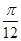 ,kπ+
,kπ+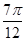 ],k∈Z.
],k∈Z.(2)y=2sin(2x+
 )―→y=2sin(2x+
)―→y=2sin(2x+ -2m),
-2m),∵y=2sin(2x+
 -2m)的图象关于直线x=
-2m)的图象关于直线x=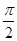 对称,
对称,∴2·
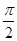 +
+ -2m=kπ+
-2m=kπ+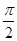 (k∈Z),
(k∈Z),∴m=-
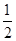 kπ+
kπ+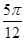 (k∈Z),
(k∈Z),当k=0时,m的最小正值为
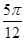 .
.
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
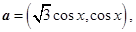 向量
向量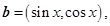 记
记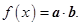
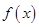 的单调递增区间;
的单调递增区间;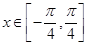 ,求函数
,求函数 )的图象,只需要将函数y=3cos2x的图象( )
)的图象,只需要将函数y=3cos2x的图象( ) 个单位
个单位 个单位
个单位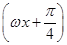 (x∈R,ω>0)的最小正周期为π,将y=f(x)的图象向左平移|φ|个单位长度,所得图象关于y轴对称,则φ的一个值是( )
(x∈R,ω>0)的最小正周期为π,将y=f(x)的图象向左平移|φ|个单位长度,所得图象关于y轴对称,则φ的一个值是( )



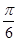 个单位,所得到的函数是偶函数;
个单位,所得到的函数是偶函数;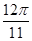 )<f(
)<f(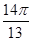 );
);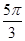 -x).
-x).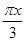 -
- )-2cos2
)-2cos2 .
.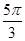 对称,则实数a的值为( )
对称,则实数a的值为( )



 与
与 在区间
在区间 上截曲线
上截曲线 所得的弦长相等且不为零,则下列描述正确的是( )
所得的弦长相等且不为零,则下列描述正确的是( )



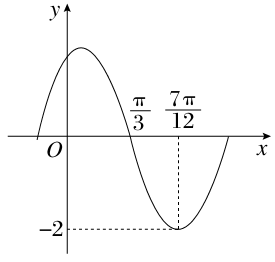
 的部分图象如图所示,则
的部分图象如图所示,则 +
+ 的值等于 .
的值等于 . 