题目内容
设函数f(x)=sin(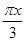 -
- )-2cos2
)-2cos2 .
.
(1)求y=f(x)的最小正周期及单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最大值.
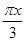 -
- )-2cos2
)-2cos2 .
.(1)求y=f(x)的最小正周期及单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最大值.
(1)6 [6k-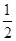 ,6k+
,6k+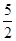 ],k∈Z
],k∈Z
(2)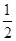
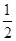 ,6k+
,6k+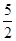 ],k∈Z
],k∈Z(2)
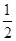
解:(1)由题意知f(x)=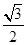 sin
sin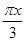 -
- cos
cos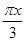 -1=
-1=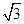 ·sin(
·sin(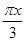 -
- )-1,所以y=f(x)的最小正周期T=
)-1,所以y=f(x)的最小正周期T=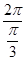 =6.
=6.
由2kπ-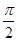 ≤
≤ x-
x- ≤2kπ+
≤2kπ+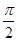 ,k∈Z,得6k-
,k∈Z,得6k-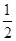 ≤x≤6k+
≤x≤6k+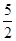 ,k∈Z,
,k∈Z,
所以y=f(x)的单调递增区间为[6k-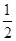 ,6k+
,6k+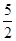 ],k∈Z.
],k∈Z.
(2)因为函数y=g(x)与y=f(x)的图象关于直线x=2对称,所以当x∈[0,1]时,y=g(x)的最大值即为x∈[3,4]时,y=f(x)的最大值,
当x∈[3,4]时, x-
x- ∈[
∈[ π,π],sin(
π,π],sin( x-
x- )∈[0,
)∈[0,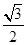 ],f(x)∈[-1,
],f(x)∈[-1,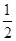 ],
],
即此时y=g(x)的最大值为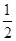 .
.
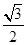 sin
sin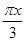 -
- cos
cos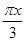 -1=
-1=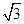 ·sin(
·sin(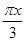 -
- )-1,所以y=f(x)的最小正周期T=
)-1,所以y=f(x)的最小正周期T=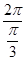 =6.
=6.由2kπ-
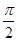 ≤
≤ x-
x- ≤2kπ+
≤2kπ+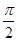 ,k∈Z,得6k-
,k∈Z,得6k-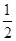 ≤x≤6k+
≤x≤6k+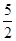 ,k∈Z,
,k∈Z,所以y=f(x)的单调递增区间为[6k-
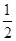 ,6k+
,6k+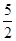 ],k∈Z.
],k∈Z.(2)因为函数y=g(x)与y=f(x)的图象关于直线x=2对称,所以当x∈[0,1]时,y=g(x)的最大值即为x∈[3,4]时,y=f(x)的最大值,
当x∈[3,4]时,
 x-
x- ∈[
∈[ π,π],sin(
π,π],sin( x-
x- )∈[0,
)∈[0,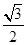 ],f(x)∈[-1,
],f(x)∈[-1,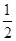 ],
],即此时y=g(x)的最大值为
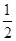 .
.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 ,若直线
,若直线 是函数
是函数 图象的一条切线.
图象的一条切线. 、
、 的横坐标依次为2和4,
的横坐标依次为2和4, 为坐标原点,求△
为坐标原点,求△ 的面积.
的面积. )(ω>0)的图象向右平移
)(ω>0)的图象向右平移 个单位长度后,与函数y=sin(ωx+
个单位长度后,与函数y=sin(ωx+ )的图象重合,则ω的最小值为________.
)的图象重合,则ω的最小值为________. )-
)-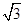 sin2x+sinxcosx.
sin2x+sinxcosx.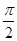 对称,求m的最小正值.
对称,求m的最小正值.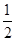 cos(ωx+φ)对任意的x∈R,都有f(
cos(ωx+φ)对任意的x∈R,都有f(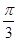 -x)=f(
-x)=f( ,cos
,cos
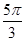

 在函数
在函数 的图象上移动,动点
的图象上移动,动点 满足
满足 ,则动点
,则动点 的轨迹方程为( )
的轨迹方程为( )




 的一个对称中心是
的一个对称中心是 ,则
,则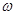 的最小值是 。
的最小值是 。