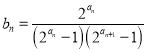جâؤ؟ؤعبف
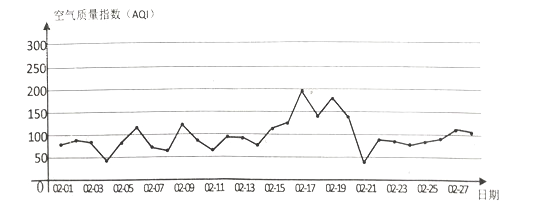
،¾جâؤ؟،؟خهز»½عئع¼ن£¬ؤ³ةج³،خھخüز¹ث؟حدû·رحئ³ِز»دîسإ»ف»î¶¯£¬»î¶¯¹وشٍبçدآ£؛دû·ر¶îأ؟آْ100شھ؟ة×ھ¶¯بçح¼ثùت¾µؤ×ھإجز»´خ£¬²¢»ٌµأدàس¦½ً¶îµؤ·µب¯£®£¨¼ظ¶¨ض¸صëµب؟ةؤـµطح£شعبخز»خ»ضأ£¬ض¸صëآنشعاّسٍµؤ±ك½çت±£¬ضطذآ×ھز»´خ£©ض¸صëثùشعµؤاّسٍ¼°¶شس¦µؤ·µ„»½ً¶î¼û±ي£®
ہبç£؛دû·ر218شھ£¬؟ة×ھ¶¯×ھإج2´خ£¬ثù»ٌµأµؤ·µب¯½ً¶îتاء½´خ½ً¶îض®؛ح£®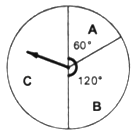
£¨1£©زرضھ¹ث؟ح¼×دû·ر؛َ»ٌµأn´خ×ھ¶¯×ھإجµؤ»ْ»ل£¬زرضھثûأ؟×ھز»´خ×ھإجض¸صëآنشعاّسٍ±ك½çµؤ¸إآتخھp£¬أ؟´خ×ھ¶¯×ھإجµؤ½ل¹ûد໥¶ہء¢£¬ةè¦خخھ¹ث؟ح¼××ھ¶¯×ھإجض¸صëآنشعاّسٍ±ك½çµؤ´خت£¬¦خµؤتر§ئعحûE¦خ= ![]() £¬·½²îD¦خ=
£¬·½²îD¦خ= ![]() £¬اَn،¢pµؤضµ£»
£¬اَn،¢pµؤضµ£»
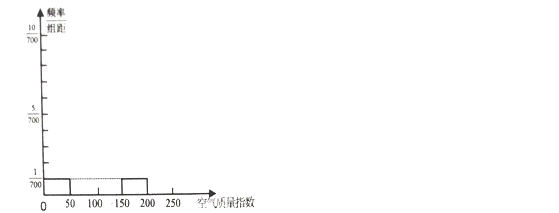
£¨2£©¹ث؟حززدû·ر280شھ£¬²¢°´¹وشٍ²خسëءث»î¶¯£¬ثû»ٌµأ·µب¯µؤ½ً¶î¼اخھ¦ا£¨شھ£©£®اَثو»ْ±نء؟¦اµؤ·ض²¼ءذ؛حتر§ئعحû£®
ض¸صëخ»ضأ | Aاّسٍ | Bاّسٍ | Cاّسٍ |
·µب¯½ً¶î£¨µ¥خ»£؛شھ£© | 60 | 30 | 0 |
،¾´ً°¸،؟
£¨1£©½â£؛زہجâزâضھ£¬¦خ·´س¶دî·ض²¼¦خ،«B£¨n£¬p£©£¬
،à ![]() £¬
£¬
سض ![]() £¬
£¬
ءھء¢½âµأ£؛ ![]() £®
£®
£¨2£©½â£؛ةèض¸صëآنشعA£¬B£¬Cاّسٍ·ض±ً¼اخھتآ¼A£¬B£¬C£®
شٍ ![]() £®
£®
سةجâزâµأ£¬¸أ¹ث؟ح؟ة×ھ¶¯×ھإج2´خ£®
ثو»ْ±نء؟¦اµؤ؟ةؤـضµخھ0£¬30£¬60£¬90£¬120£®
![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
،àثو»ْ±نء؟¦اµؤ·ض²¼ءذخھ£؛
P | 0 | 30 | 60 | 90 | 120 |
¦ا |
|
|
|
|
|
ئنتر§ئعحû ![]()
،¾½âخِ،؟£¨1£©زہجâزâضھ£¬¦خ·´س¶دî·ض²¼¦خ،«B£¨n£¬p£©£¬سة´ثہûسأ¶دî·ض²¼µؤذشضتؤـاَ³ِn،¢pµؤضµ£®£¨2£©ةèض¸صëآنشعA£¬B£¬Cاّسٍ·ض±ً¼اخھتآ¼A£¬B£¬C£®شٍ ![]() £®سةجâزâµأ£¬¸أ¹ث؟ح؟ة×ھ¶¯×ھإج2´خ£®ثو»ْ±نء؟¦اµؤ؟ةؤـضµخھ0£¬30£¬60£¬90£¬120£¬·ض±ًاَ³ِدàس¦µؤ¸إآت£¬سة´ثؤـاَ³ِثو»ْ±نء؟¦اµؤ·ض²¼ءذ؛حتر§ئعحû£®
£®سةجâزâµأ£¬¸أ¹ث؟ح؟ة×ھ¶¯×ھإج2´خ£®ثو»ْ±نء؟¦اµؤ؟ةؤـضµخھ0£¬30£¬60£¬90£¬120£¬·ض±ًاَ³ِدàس¦µؤ¸إآت£¬سة´ثؤـاَ³ِثو»ْ±نء؟¦اµؤ·ض²¼ءذ؛حتر§ئعحû£®
،¾؟¼µم¾«خِ،؟½â´ً´ثجâµؤ¹ط¼üشعسعہي½âہëة¢ذحثو»ْ±نء؟¼°ئن·ض²¼ءذµؤدà¹طضھت¶£¬صئخصشعةن»÷،¢²ْئ·¼ىرéµبہ×سضذ£¬¶شسعثو»ْ±نء؟X؟ةؤـب،µؤضµ£¬خزأا؟ةزش°´ز»¶¨´خذٍز»ز»ءذ³ِ£¬صâرùµؤثو»ْ±نء؟½ذ×ِہëة¢ذحثو»ْ±نء؟£®ہëة¢ذحثو»ْ±نء؟µؤ·ض²¼ءذ£؛ز»°مµؤ,ةèہëة¢ذحثو»ْ±نء؟X؟ةؤـب،µؤضµخھx1,x2,.....,xi,......,xn£¬Xب،أ؟ز»¸ِضµ xi(i=1,2,......£©µؤ¸إآتP(¦خ=xi£©£½Pi£¬شٍ³ئ±يخھہëة¢ذحثو»ْ±نء؟X µؤ¸إآت·ض²¼£¬¼ٍ³ئ·ض²¼ءذ£®

 ¶ل¹ع½ً¾يب«ؤـء·؟¼دµءذ´ً°¸
¶ل¹ع½ً¾يب«ؤـء·؟¼دµءذ´ً°¸