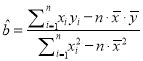��Ŀ����
����Ŀ���������ҿ�ݹ�˾�䡰���С�硱���չ��ʷ������£���˾�涨��н![]() Ԫ��ÿ�����
Ԫ��ÿ�����![]() Ԫ���ҹ�˾�涨��н
Ԫ���ҹ�˾�涨��н![]() Ԫ��ÿ��ǰ
Ԫ��ÿ��ǰ![]() ����ɣ�����
����ɣ�����![]() ���IJ���ÿ�����
���IJ���ÿ�����![]() Ԫ
Ԫ
��1������ҿ�ݹ�˾�ġ����С�硱һ�չ���![]() ����λ��Ԫ�����ͻ�����
����λ��Ԫ�����ͻ�����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ����
����![]() ��
��
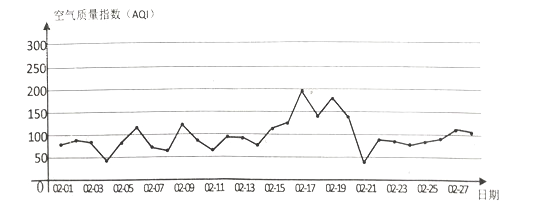
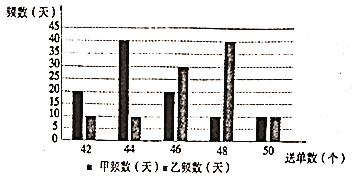
��2������ͬһ��˾�ġ����С�硱һ���ͻ�������ͬ���ִ����ҹ�˾�������ȡһ�������С�硱������¼��![]() ����ͻ��������õ���������ͼ:
����ͻ��������õ���������ͼ:
����Ƶ����Ϊ���ʣ��ش��������⣺
�ټ��ҿ�ݹ�˾�ġ����С�硱�չ���Ϊ![]() ����λ��Ԫ������
����λ��Ԫ������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
��С������ҹ�˾�е�һ��ӦƸ�����С�硱�Ĺ������������������ĽǶȿ��ǣ�����������ѧ��ͳ��ѧ֪ʶΪ������ѡ��˵������.
���𰸡���1���ף� ![]() ���ң�
���ң� 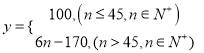 ��2���ټ��������Ƽ�С��ȥ�ҿ�ݹ�ʽӦƸ.
��2���ټ��������Ƽ�С��ȥ�ҿ�ݹ�ʽӦƸ.
�������������������1���ɷֶκ�����д�������С���ͻ������빤�ʵĺ�����ϵʽ����2����������ͳ��ͼ�ɵ�![]() �Ŀ���ȡֵ��Χ��������Ӧ�ĸ���ֵ���ɵ÷ֲ��У���һ���������ѧ�������ڿ���������ݹ�˾�Ŀ��С�����ƽ�����ʣ��Ƽ�С��ȥƽ�����ʽϸߵĹ�˾�ϰ࣮
�Ŀ���ȡֵ��Χ��������Ӧ�ĸ���ֵ���ɵ÷ֲ��У���һ���������ѧ�������ڿ���������ݹ�˾�Ŀ��С�����ƽ�����ʣ��Ƽ�С��ȥƽ�����ʽϸߵĹ�˾�ϰ࣮
�����������1����ݹ�ʽ�ġ����С�硱һ�չ���![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��
![]()
�ҿ�ݹ�ʽ�ġ����С�硱һ�չ���![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��
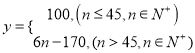 .
.
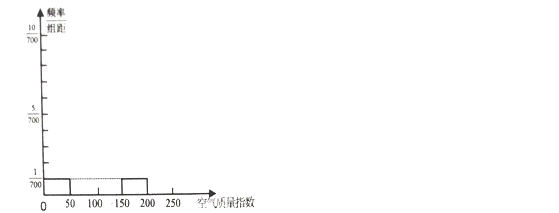
��2���ټ��ҿ�ݹ�˾�ġ����С�硱�չ���Ϊ![]() ����λ��Ԫ����������ͼ��
����λ��Ԫ����������ͼ��![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ��
��
![]()
![]() ��
��
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��

���ҿ�ݹ�˾�ġ����С�硱��ƽ���͵���Ϊ�� ![]() ��
��
�����ҿ�ݹ�˾�ġ����С�硱��ƽ������Ϊ![]() ��Ԫ����
��Ԫ����
�ɢ�֪����ݹ�˾�ġ����С�硱��ƽ������Ϊ![]() Ԫ.
Ԫ.
���Ƽ�С��ȥ�ҿ�ݹ�ʽӦƸ.