Question

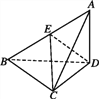
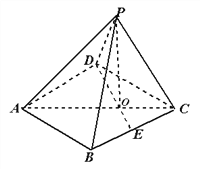
【题目】如图，已知四棱锥的底面的菱形， ，点E是BC边的中点，AC和DE交于点O，PO ；

（1）求证： ；

（2） 求二面角P-AD-C的大小。

（3）在（2）的条件下，求异面直线PB与DE所成角的余弦值。

Answer 1

【答案】（1）见解析；（2）二面角的大小为；（3）异面直线、所成角的余弦值为。

【解析】试题分析：

(1)由题意可证得，结合射影定理可证得；

(2)由题意找到二面角的平面角，结合三角函数值可得二面角的大小为.

(3)利用平移法结合余弦定理可得异面直线、所成角的余弦值为.

试题解析：

（1）在菱形中，连接则是等边三角形。

点是边的中点

平面

是斜线在底面内的射影

（2）

菱形中,

又平面, 是在平面内的射影

为二面角的平面角

在菱形中, ，由（1）知， 等边三角形

点是边的中点， 与互相平分

点是的重心

又在等边三角形中，

所以在中，

二面角的大小为.

(3)取中点，连结，

则

与所成角与所成角

连结

平面, 、平面

在中,

在中,

在中,

由（2）可知，

设与所成的角为

则

所以异面直线、所成角的余弦值为