题目内容
【题目】已知等腰梯形![]() 中(如图1),
中(如图1),![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的点,
上的点, ![]() ,现将四边形
,现将四边形![]() 沿
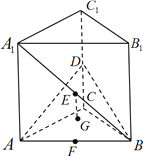
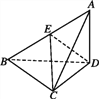
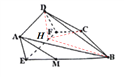
沿![]() 折起(如图2).
折起(如图2).
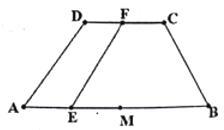
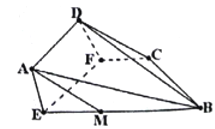
图1 图2
⑴求证: ![]() 平面
平面![]() ;
;
⑵在图2中,若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接![]() ,由
,由![]() 可得
可得![]() ,即可证
,即可证![]() ∥
∥![]() 且
且![]() ,然后即可证出四边形
,然后即可证出四边形![]() 为平行四边形,进而可证明
为平行四边形,进而可证明![]() 平面
平面![]() ;(2)作
;(2)作![]() 于
于![]() ,连接
,连接![]() ,在
,在![]() 中,可得
中,可得![]() ,在
,在![]() 中,可得
中,可得![]() ,结合
,结合![]() ,推出
,推出![]() ,再由
,再由![]() ,推出
,推出![]() 平面
平面![]() ,即可得到
,即可得到![]() 为
为![]() 与平面
与平面![]() 所成的角,再根据余弦定理得出
所成的角,再根据余弦定理得出![]() ,进而可求出
,进而可求出![]() 的值,即直线
的值,即直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:(1)证明:连接![]()
∵![]()
∴![]()
∴![]() ∥
∥![]() ,且
,且![]()
又∵![]() ∥
∥![]() ,且
,且![]()
∴![]() ∥
∥![]() ,且
,且![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]() ∥
∥![]()
又∵![]() 面
面![]() ,
, ![]() 面
面![]()
∴![]() ∥面
∥面![]()
(2)作![]() 于
于![]() ,连接
,连接![]() ,在
,在![]() 中,易知
中,易知![]() ,而
,而![]()
∴![]() ,
, ![]()
在![]() 中,
中, ![]() ,易知
,易知![]()
又∵![]()
∴![]()
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]()
∴![]()
∴![]()
又∵![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() 平面
平面![]()
∴![]() 为
为![]() 在平面
在平面![]() 内的射影
内的射影
∴![]() 为
为![]() 与平面
与平面![]() 所成的角
所成的角
在![]() 中,易知
中,易知![]()
∴![]()
在![]() 中,
中, ![]()
∴![]() ,即
,即![]() 与平面
与平面![]() 的所成的角的正弦值为
的所成的角的正弦值为![]() .
.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目