Question

【题目】选修4一5:不等式选讲.

已知函数.

（1）求的解集；

（2）设函数，若对任意的都成立，求实数的取值范围.

Answer 1

【答案】（1）或.（2）

【解析】试题分析：（1）函数f（x）=|x-3|+|x+4|，不等式f（x）≥f（4）即|x-3|+|x+4|≥9．可得①或②或③

分别求得①、②、③的解集，再取并集，即得所求；
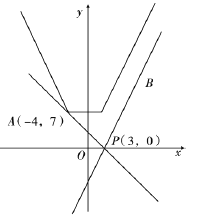
（2）由题意可得，f（x）的图象恒在g（x）图象的上方，作函数y=f（x）和 y=g（x）的图象如图，由kPB=2，A（-4，7），可得kPA=-1，数形结合求得实数k的取值范围．

试题解析：

（1） ，

∴，即，

∴①或②或③

解得不等式①：；②：无解；③： ，

所以的解集为或.

（2）即的图象恒在图象的上方，

可以作出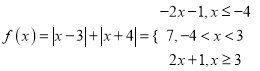的图象，

而图象为恒过定点，且斜率变化的一条直线，

作出函数图象如图，其中，

，∴，由图可知，要使得的图象恒在图象的上方，实数的取值范围应该为.