题目内容
已知函数f(x)=|ax-2|+bln x(x>0,实数a,b为常数).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程f(x)= 在(0,1]上解的个数.
在(0,1]上解的个数.
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程f(x)=
 在(0,1]上解的个数.
在(0,1]上解的个数.(1)[2,+∞).
(2)0
(2)0
解:(1)当a=1时,
f(x)=|x-2|+bln x
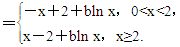
①当0<x<2时,f(x)=-x+2+bln x,
f′(x)=-1+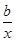 .
.
由条件得-1+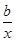 ≥0恒成立,即b≥x恒成立.
≥0恒成立,即b≥x恒成立.
所以b≥2;
②当x≥2时,f(x)=x-2+bln x,
f′(x)=1+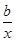 .
.
由条件得1+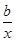 ≥0恒成立,即b≥-x恒成立.
≥0恒成立,即b≥-x恒成立.
所以b≥-2.
因为函数f(x)的图像在(0,+∞)上不间断,综合①②得b的取值范围是[2,+∞).
(2)令g(x)=|ax-2|+ln x- ,即
,即
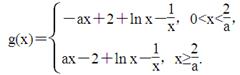
当0<x<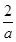 时,
时,
g(x)=-ax+2+ln x- ,
,
g′(x)=-a+ +
+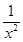 .
.
因为0<x<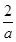 ,所以
,所以 >
>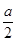 ,
,
则g′(x)>-a+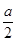 +
+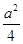 =
=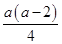 ≥0,
≥0,
即g′(x)>0,所以g(x)在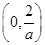 上是单调增函数;
上是单调增函数;
当x>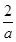 时,g(x)=ax-2+ln x-
时,g(x)=ax-2+ln x- ,
,
g′(x)=a+ +
+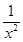 >0,
>0,
所以g(x)在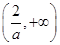 上是单调增函数.
上是单调增函数.
因为函数g(x)的图像在(0,+∞)上不间断,所以g(x)在(0,+∞)上是单调增函数.
因为g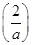 =ln
=ln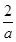 -
-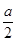 ,
,
而a≥2,所以ln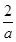 ≤0,则g
≤0,则g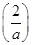 <0,
<0,
g(1)=|a-2|-1=a-3.
①当a≥3时,因为g(1)≥0,所以g(x)=0在(0,1]上有唯一解,即方程f(x)= 解的个数为1;
解的个数为1;
②当2≤a<3时,因为g(1)<0,所以g(x)=0在(0,1]上无解,即方程f(x)= 解的个数为0.
解的个数为0.
f(x)=|x-2|+bln x
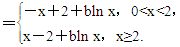
①当0<x<2时,f(x)=-x+2+bln x,
f′(x)=-1+
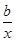 .
.由条件得-1+
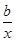 ≥0恒成立,即b≥x恒成立.
≥0恒成立,即b≥x恒成立.所以b≥2;
②当x≥2时,f(x)=x-2+bln x,
f′(x)=1+
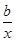 .
.由条件得1+
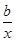 ≥0恒成立,即b≥-x恒成立.
≥0恒成立,即b≥-x恒成立.所以b≥-2.
因为函数f(x)的图像在(0,+∞)上不间断,综合①②得b的取值范围是[2,+∞).
(2)令g(x)=|ax-2|+ln x-
 ,即
,即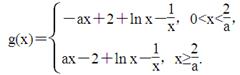
当0<x<
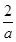 时,
时,g(x)=-ax+2+ln x-
 ,
,g′(x)=-a+
 +
+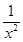 .
.因为0<x<
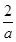 ,所以
,所以 >
>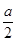 ,
,则g′(x)>-a+
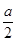 +
+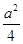 =
=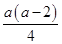 ≥0,
≥0,即g′(x)>0,所以g(x)在
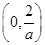 上是单调增函数;
上是单调增函数;当x>
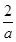 时,g(x)=ax-2+ln x-
时,g(x)=ax-2+ln x- ,
,g′(x)=a+
 +
+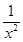 >0,
>0,所以g(x)在
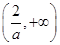 上是单调增函数.
上是单调增函数.因为函数g(x)的图像在(0,+∞)上不间断,所以g(x)在(0,+∞)上是单调增函数.
因为g
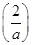 =ln
=ln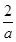 -
-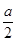 ,
,而a≥2,所以ln
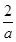 ≤0,则g
≤0,则g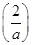 <0,
<0,g(1)=|a-2|-1=a-3.
①当a≥3时,因为g(1)≥0,所以g(x)=0在(0,1]上有唯一解,即方程f(x)=
 解的个数为1;
解的个数为1;②当2≤a<3时,因为g(1)<0,所以g(x)=0在(0,1]上无解,即方程f(x)=
 解的个数为0.
解的个数为0.
练习册系列答案
相关题目
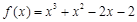 的一个正数零点附近的函数值用二分法计算,得数据如下:
的一个正数零点附近的函数值用二分法计算,得数据如下: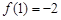
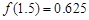
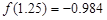
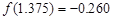
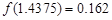
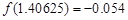
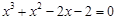 的一个最接近的近似根为( )
的一个最接近的近似根为( )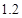 B.
B.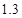 C.
C.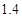 D.
D.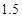
 有极值点
有极值点 ,且
,且 ,则关于
,则关于 的方程
的方程 的不同实根的个数是( )
的不同实根的个数是( ) ,4)
,4) )
)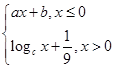 的图象如图所示,则a+b+c=________.
的图象如图所示,则a+b+c=________.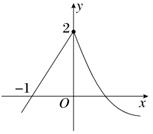
 则函数f(x)=sgn(ln x)-ln2x的零点个数为________.
则函数f(x)=sgn(ln x)-ln2x的零点个数为________.