题目内容
关于x的二次方程x2+(m-1)x+1=0在区间[0,2]上有解,求实数m的取值范围.
(-∞,-1)
解:设f(x)=x2+(m-1)x+1,x∈[0,2],
①若f(x)=0在区间[0,2]上有一解,
∵f(0)=1>0,则应有f(2)<0,
又∵f(2)=22+(m-1)×2+1,
∴m<-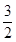 .
.
②若f(x)=0在区间[0,2]上有两解,则
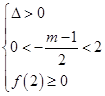
∴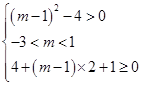
∴
∴-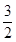 ≤m<-1.
≤m<-1.
由①②可知m的取值范围(-∞,-1).
①若f(x)=0在区间[0,2]上有一解,
∵f(0)=1>0,则应有f(2)<0,
又∵f(2)=22+(m-1)×2+1,
∴m<-
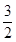 .
.②若f(x)=0在区间[0,2]上有两解,则
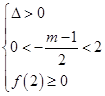
∴
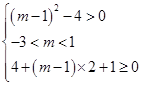
∴

∴-
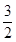 ≤m<-1.
≤m<-1.由①②可知m的取值范围(-∞,-1).

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
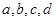 是不全为
是不全为 的实数,函数
的实数,函数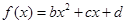 ,
,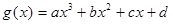 ,方程
,方程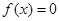 有实根,且
有实根,且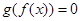 的根,反之,
的根,反之,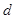 的值;(2)若
的值;(2)若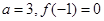 ,求
,求 的取值范围.
的取值范围.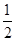 )x+
)x+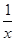 的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( )
的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( ) 在(0,1]上解的个数.
在(0,1]上解的个数.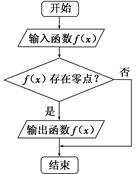
 =2;
=2;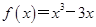 的图象与直线
的图象与直线 有相异三个公共点,则
有相异三个公共点,则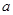 的取值范围是(-2,2)
的取值范围是(-2,2)