题目内容
20．我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”．已知F1，F2是一对相关曲线的焦点，P是椭圆和双曲线在第一象限的交点，当∠F1PF2=60°时，这一对相关曲线中椭圆的离心率为（ ）| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{1}{2}$ |
分析 设F1P=m，F2P=n，F1F2=2c，由余弦定理4c2=m2+n2-mn，设a1是椭圆的长半轴，a1是双曲线的实半轴，由椭圆及双曲线定义，得m+n=2a1，m-n=2a1，由此能求出结果．
解答 解：设F1P=m，F2P=n，F1F2=2c，
由余弦定理得（2c）2=m2+n2-2mncos60°，即4c2=m2+n2-mn，
设a1是椭圆的实半轴，a2是双曲线的实半轴，
由椭圆及双曲线定义，得m+n=2a1，m-n=2a2，
∴m=a1+a2，n=a1-a2，
将它们及离心率互为倒数关系代入前式得3a22-4c2+a12=0，
a1=3a2，e1•e2=$\frac{c}{{a}_{1}}•\frac{c}{{a}_{2}}$=$\frac{c}{{a}_{1}}•\frac{3c}{{a}_{1}}$=1
即3e12=1
∴e1=$\frac{\sqrt{3}}{3}$
故选：A．
点评 本题考查椭圆与双曲线的定义，考查了椭圆与双曲线的几何性质，是基础题．
练习册系列答案
相关题目
8．已知实数x∈[1，10]执行如图所示的流程图，则输出的x不小于63的概率为（ ）
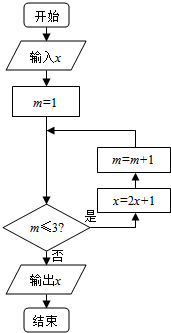
| A． | $\frac{1}{3}$ | B． | $\frac{4}{9}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{10}$ |
15．若?x∈[$\frac{1}{4}$，+∞），使得不等式ex＜$\frac{x-m}{\sqrt{x}}$成立，则实数m的取值范围是（ ）
| A． | （-∞，-$\frac{1}{2}$${e}^{\frac{1}{4}}$） | B． | （$\frac{1}{4}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$，+∞） | C． | （-∞，$\frac{1}{4}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$） | D． | （$\frac{1}{2}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$，+∞） |
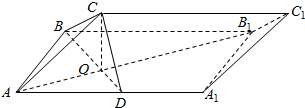如图，在三棱柱ABC-A1B1C1中，面ABB1A1为矩形，AB=1，AA1=$\sqrt{2}$，D为AA1的中点，BD与AB1交于点O，CO⊥面ABB1A1．