题目内容
1．定义在实数集R上的函数f（x），对定义域内任意x满足f（x+2）-f（x-3）=0，且在区间（-1，4]上f（x）=x2-2x，则函数f（x）在区间（0，2015]上的零点个数为（ ）| A． | 403 | B． | 806 | C． | 1209 | D． | 1208 |
分析 由ff（x+2）-f（x-3）=0，得到函数的周期是5，分别画出y=x2，y=2x的图象，由图象可知f（x）在（-1，4]上有3个零点，故f（x）在（0，5]上有3个零点利用函数的周期性即可求出函数y=f（x）在区间[0，2015]上零点个数．
解答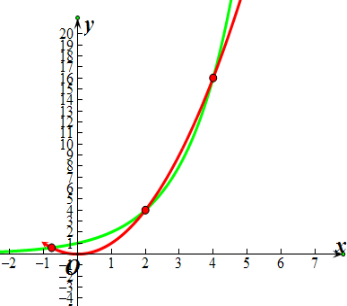 
解：∵f（x+2）-f（x-3）=0，
令x=x+3，
则f（x+5）=f（x+3-3）=f（x），
∴函数的周期是5．
分别画出y=x2，y=2x的图象，如图所示，
在（-1，4]上有3个交点，
∴f（x）在（-1，4]上有3个零点，
∴f（x）在（0，5]上有3个零点，
∵2015=403×5，
∴函数f（x）在区间（0，2015]上的零点个数为403×3=1209．
故选：C．
点评 本题主要考查函数零点的个数的判断，函数的周期性，函数的图象和性质，利用函数的周期性是解决本题的关键，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在三棱柱ABC-A1B1C1中，面ABB1A1为矩形，AB=1，AA1=$\sqrt{2}$，D为AA1的中点，BD与AB1交于点O，CO⊥面ABB1A1．
6．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=-1，且|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |
13．函数f（x）=Asin（ωx+θ）（A＞0，ω＞0）的部分图象如图所示，则f（$\frac{π}{3}$）的值为（ ）
| A． | $\sqrt{2}$ | B． | 0 | C． | $\frac{\sqrt{6}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |